[题目]如图.四棱锥中.底面为平行四边形.底面 .(I)证明:(II)设.求棱锥的高. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】如图，四棱锥中，底面为平行四边形.底面 .

（I）证明：

（II）设，求棱锥的高.

【答案】（Ⅰ ）见解析；（Ⅱ）的高为。

【解析】

(I)本小题的关键是证明,进而证明即可.

(II)求棱锥D-PBC的高实质就是求点D到平面PBC的距离,可以考虑体积法,利用来求.

（Ⅰ）因为，由余弦定理得

从而BD2+AD2= AB2，故BDAD又PD底面ABCD，可得BDPD

所以BD平面PAD. 故 PABD…………5 分

（Ⅱ）如图，作DEPB，垂足为E．已知PD底面ABCD，则PDBC．由（Ⅰ）知BDAD，又BC//AD，所以BCBD．故BC平面PBD，BCDE．则DE平面PBC．

由题设知，PD=1，则BD=，PB=2，根据BE·PB=PD·BD，得DE=，

即棱锥D—PBC的高为…………12 分

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知函数f（x）=xlnx．
（Ⅰ）设函数g（x）= ，求g（x）的单调区间；
（Ⅱ）若方程f（x）=t有两个不相等的实数根x1 ， x2 ，求证：x1+x2 ．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）=x2﹣2x+a（ex﹣1+e﹣x+1）有唯一零点，则a=（）
A.﹣
B.
C.
D.1

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）=|x+1|﹣|x﹣2|．
（Ⅰ）求不等式f（x）≥1的解集；
（Ⅱ）若不等式f（x）≥x2﹣x+m的解集非空，求m的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】一网站营销部为统计某市网友2017年12月12日在某网店的网购情况，随机抽查了该市60名网友在该网店的网购金额情况，如下表：

网购金额(单位：千元)	频数	频率	网购金额(单位：千元)	频数	频率
[0,0.5)	3	0.05	[1.5,2)	15	0.25
[0.5,1)			[2,2.5)	18	0.30
[1,1.5)	9	0.15	[2.5,3]

若将当日网购金额不小于2千元的网友称为“网购达人”，网购金额小于2千元的网友称为“网购探者”，已知“网购达人”与“网购探者”人数的比例为2:3.

（1）确定，，，的值，并补全频率分布直方图；

（2）①.试根据频率分布直方图估算这60名网友当日在该网店网购金额的平均数和中位数；

②.若平均数和中位数至少有一个不低于2千元，则该网店当日评为“皇冠店”，试判断该网店当日能否被评为“皇冠店”.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】[选修4-4：坐标系与参数方程]
在直角坐标系xOy中，直线l1的参数方程为，（t为参数），直线l2的参数方程为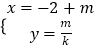，（m为参数）．设l1与l2的交点为P，当k变化时，P的轨迹为曲线C．（10分）
（1）写出C的普通方程；
（2）以坐标原点为极点，x轴正半轴为极轴建立极坐标系，设l3：ρ（cosθ+sinθ）﹣ =0，M为l3与C的交点，求M的极径．