
【题目】已知集合M是满足下列性质的函数![]() 的全体:在定义域
的全体:在定义域![]() 内存在
内存在![]() ,使函数
,使函数![]() 成立;
成立;
(1)请给出一个![]() 的值,使函数
的值,使函数![]()
(2)函数![]() 是否是集合M中的元素?若是,请求出所有
是否是集合M中的元素?若是,请求出所有![]() 组成的集合;若不是,请说明理由;
组成的集合;若不是,请说明理由;
(3)设函数![]() ,求实数a的取值范围.
,求实数a的取值范围.
【答案】(1)![]() =2;(2)是,
=2;(2)是,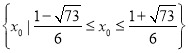 (3)
(3)![]() 或
或![]()
【解析】
(1)利用![]() 列不等式,由此求得
列不等式,由此求得![]() 的一个取值.
的一个取值.
(2)假设存在![]() 符合题意,验证
符合题意,验证![]() ,由此判断出
,由此判断出![]() 的所有可能取值.
的所有可能取值.
(3)利用![]() 列不等式,对
列不等式,对![]() 分成
分成![]() 三种情况进行分类讨论,由此求得
三种情况进行分类讨论,由此求得![]() 的取值范围.
的取值范围.
(1)当![]() 时,依题意在定义域
时,依题意在定义域![]() 内存在
内存在![]() ,使函数
,使函数![]() 成立,而
成立,而![]() ,即
,即![]() ,即
,即![]() ,故可取
,故可取![]() ,此时
,此时![]() .
.
(2)假设存在![]() 符合题意,而
符合题意,而![]() ,即
,即![]() ,即
,即![]() ,化简得
,化简得![]() ,解得
,解得![]() .所以函数
.所以函数![]() 是集合M中的元素,且
是集合M中的元素,且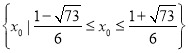 .
.
(3)由于函数![]() ,
,![]() ,由
,由![]() ,得
,得![]() ①,
①,![]() .
.
当![]() 时,①成立.
时,①成立.
当![]() 时,①的左边为负数,右边为正数,即①成立.
时,①的左边为负数,右边为正数,即①成立.
当![]() 时,①可化为
时,①可化为![]() ,也即存在
,也即存在![]() ,使
,使![]() ②成立.
②成立.
当![]() 时,显然存在
时,显然存在![]() ,使②成立;
,使②成立;
当![]() 时,②化为
时,②化为![]() ,显然存在
,显然存在![]() ,使②成立.
,使②成立.
当![]() ,即
,即![]() 时,不等式
时,不等式![]() 对应的一元二次方程
对应的一元二次方程![]() ,开口向下,且判别式
,开口向下,且判别式![]()
![]() ,由于
,由于![]() ,所以
,所以![]() ,所以不存在
,所以不存在![]() ,使②成立.
,使②成立.
综上所述,实数![]() 的取值范围是
的取值范围是![]() 或
或![]() .
.


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:高中数学 来源: 题型:
【题目】2018年双11当天,某购物平台的销售业绩高达2135亿人民币.与此同时,相关管理部门推出了针对电商的商品和服务的评价体系,现从评价系统中选出200次成功交易,并对其评价进行统计,对商品的好评率为0.9,对服务的好评率为0.75,其中对商品和服务都做出好评的交易为140次.
(1)请完成下表,并判断是否可以在犯错误概率不超过0.5%的前提下,认为商品好评与服务好评有关?
对服务好评 | 对服务不满意 | 合计 | |
对商品好评 | 140 | ||
对商品不满意 | 10 | ||
合计 | 200 |
(2)若将频率视为概率,某人在该购物平台上进行的3次购物中,设对商品和服务全好评的次数为X.
①求随机变量X的分布列;
②求X的数学期望和方差.
附:![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】绝对值|x﹣1|的几何意义是数轴上的点x与点1之间的距离,那么对于实数a,b,![]() 的几何意义即为点x与点a、点b的距离之和.
的几何意义即为点x与点a、点b的距离之和.
(1)直接写出![]() 与
与![]() 的最小值,并写出取到最小值时x满足的条件;
的最小值,并写出取到最小值时x满足的条件;
(2)设a1≤a2≤…≤an是给定的n个实数,记S=![]() .试猜想:若n为奇数,则当x∈ 时S取到最小值;若n为偶数,则当x∈ 时,S取到最小值;(直接写出结果即可)
.试猜想:若n为奇数,则当x∈ 时S取到最小值;若n为偶数,则当x∈ 时,S取到最小值;(直接写出结果即可)
(3)求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥B-AEDC中,平面AEDC⊥平面ABC,F为BC的中点,P为BD的中点,且AE//DC,∠ACD=∠BAC=90°,DC=AC=AB=2AE
(1)证明:EP⊥平面BCD;
(2)若DC=2,求三棱锥E-BDF的体积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,曲线![]() ,
,![]() ,C与l有且仅有一个公共点.
,C与l有且仅有一个公共点.
(Ⅰ)求a;
(Ⅱ)O为极点,A,B为C上的两点,且![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在正方形![]() 中,
中,![]() 是
是![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上,且
上,且![]() .若将
.若将![]() 分别沿
分别沿![]() 折起,使
折起,使![]() 两点重合于点
两点重合于点![]() ,如图2.
,如图2.
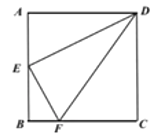
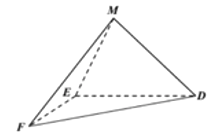
图1 图2
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com