
【题目】在△ABC中,设内角A、B、C的对边分别为a、b、c,向量 ![]() =(cosA+
=(cosA+ ![]() ,sinA),向量
,sinA),向量 ![]() =(﹣sinA,cosA),若|
=(﹣sinA,cosA),若| ![]() +
+ ![]() |=2.
|=2.
(1)求角A的大小;
(2)若b=4 ![]() ,且c=
,且c= ![]() a,求△ABC的面积.
a,求△ABC的面积.
【答案】
(1)解:∵ ![]() +
+ ![]() =(cosA+
=(cosA+ ![]() ﹣sinA,cosA+sinA),
﹣sinA,cosA+sinA),
∴| ![]() +
+ ![]() |2=(cosA+
|2=(cosA+ ![]() ﹣sinA)2+(cosA+sinA)2,
﹣sinA)2+(cosA+sinA)2,
=2+2 ![]() (cosA﹣sinA)+(cosA﹣sinA)2+(cosA+sinA)2
(cosA﹣sinA)+(cosA﹣sinA)2+(cosA+sinA)2
=2+2 ![]() (cosA﹣sinA)+2
(cosA﹣sinA)+2
=4﹣4sin(A﹣ ![]() ),
),
∵| ![]() +
+ ![]() |=2,
|=2,
∴4sin(A﹣ ![]() )=0,
)=0,
又∵0<A<π,
∴﹣ ![]() <A﹣
<A﹣ ![]() <
< ![]() ,
,
∴A﹣ ![]() =0,
=0,
∴A= ![]()
(2)解:∵由余弦定理,a2=b2+c2﹣2bccosA,又b=4 ![]() ,c=
,c= ![]() a,A=
a,A= ![]() ,
,
得:a2=32+2a2﹣2×4 ![]() ×
× ![]() a
a ![]() ,
,
即:a2﹣8 ![]() a+32=0,解得a=4
a+32=0,解得a=4 ![]() ,
,
∴c=8,
∴S△ABC= ![]() bcsinA=
bcsinA= ![]() sin
sin ![]() =16
=16
【解析】(1)先根据向量模的运算表示出| ![]() +
+ ![]() |2 , 然后化简成y=Asin(wx+ρ)+b的形式,再根据正弦函数的性质和|
|2 , 然后化简成y=Asin(wx+ρ)+b的形式,再根据正弦函数的性质和| ![]() +
+ ![]() |=2可求出A的值.(2)先根据余弦定理求出a,c的值,再由三角形面积公式可得到最后答案.
|=2可求出A的值.(2)先根据余弦定理求出a,c的值,再由三角形面积公式可得到最后答案.
【考点精析】本题主要考查了正弦定理的定义和余弦定理的定义的相关知识点,需要掌握正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() 才能正确解答此题.
才能正确解答此题.


 名题金卷系列答案
名题金卷系列答案科目:高中数学 来源: 题型:
【题目】如图,多面体EF﹣ABCD中,ABCD是正方形,AC、BD相交于O,EF∥AC,点E在AC上的射影恰好是线段AO的中点.
(Ⅰ)求证:BD⊥平面ACF;
(Ⅱ)若直线AE与平面ABCD所成的角为60°,求平面DEF与平面ABCD所成角的正弦值.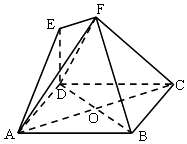
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】农科院的专家为了了解新培育的甲、乙两种麦苗的长势情况,从甲、乙两种麦苗的试验田中各抽取6株麦苗测量麦苗的株高,数据如下:(单位:cm)
甲:9,10,11,12,10,20
乙:8,14,13,10,12,21.
(1)在给出的方框内绘出所抽取的甲、乙两种麦苗株高的茎叶图;
(2)分别计算所抽取的甲、乙两种麦苗株高的平均数与方差,并由此判断甲、乙两种麦苗的长势情况.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区交管部门为了对该地区驾驶员的某项考试成绩进行分析,随机抽取了15分到45分之间的1000名学员的成绩,并根据这1000名驾驶员的成绩画出样本的频率分布直方图(如图),则成绩在[30,35)内的驾驶员人数共有( ) 
A.60
B.180
C.300
D.360
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥PABCD中,AD⊥平面PDC,AD∥BC,PD⊥PB,AD=1,BC=3,CD=4,PD=2.

(1)求异面直线AP与BC所成角的余弦值;
(2)求证:PD⊥平面PBC;
(3)求直线AB与平面PBC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,![]() 为正方体,给出以下五个结论:
为正方体,给出以下五个结论:
① ![]() 平面
平面![]() ;
;
② ![]() ⊥平面
⊥平面![]() ;
;
③ ![]() 与底面
与底面![]() 所成角的正切值是
所成角的正切值是![]() ;
;
④ 二面角![]() 的正切值是
的正切值是![]() ;
;
⑤ 过点![]() 且与异面直线
且与异面直线![]() 和
和 ![]() 均成70°角的直线有4条.
均成70°角的直线有4条.
其中,所有正确结论的序号为________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() :
: ![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
, ![]() 两点,记抛物线在
两点,记抛物线在![]() ,
, ![]() 两点处的切线
两点处的切线![]() ,
, ![]() 的交点为
的交点为![]() .
.
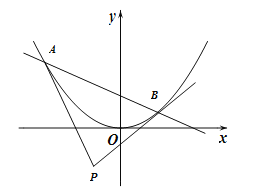
(I)求证: ![]() ;
;
(II)求点![]() 的坐标(用
的坐标(用![]() ,
, ![]() 表示);
表示);
(Ⅲ)若![]() ,求△
,求△![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将号码分别为1、2、…、9的九个小球放入一个袋中,这些小球仅号码不同,其余完全相同,甲从袋中摸出一个球.其号码为a,放回后,乙从此袋中再摸出一个球,其号码为b,则使不等式a-2b+10>0成立的事件发生的概率等于________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com