
【题目】已知函数![]() ,
,![]() ,给出如下四个命题:
,给出如下四个命题:
①![]() 的单调递增区间为
的单调递增区间为![]() ;
;
②![]() 时,
时,![]() 的极小值点为
的极小值点为![]() ;
;
③![]() 时,
时,![]() 在
在![]() 上存在唯一零点;
上存在唯一零点;
④若![]() 在
在![]() (
(![]() 为自然对数的底数)上的最小值为3,则
为自然对数的底数)上的最小值为3,则![]() .
.
其中的真命题有______.(填上你认为所有正确的结论序号
【答案】②④
【解析】
求出函数的定义域以及导函数![]() ,根据
,根据![]() 的取值范围以及函数的单调性与导数的关系可判断①;根据极小值点的定义可判断②;根据零点存在性定理可判断③;根据函数的单调性可判断④.
的取值范围以及函数的单调性与导数的关系可判断①;根据极小值点的定义可判断②;根据零点存在性定理可判断③;根据函数的单调性可判断④.
函数![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,函数在
,函数在![]() 上单调递增,
上单调递增,
当![]() 时,
时,![]() ,解得
,解得![]() ,函数
,函数![]() 的单调递增区间为
的单调递增区间为![]() ,故①错误;
,故①错误;
当![]() 时,
时,![]() ,令
,令![]() ,解得
,解得![]() ,即函数在
,即函数在![]() 上单调递增,
上单调递增,
令![]() ,解得
,解得![]() ,函数在
,函数在![]() 单调递减,
单调递减,
所以![]() 的极小值点为
的极小值点为![]() ,故②正确;
,故②正确;
当![]() 时,由
时,由![]() ,
,
当![]() 时,函数
时,函数![]() 有唯一一个零点;
有唯一一个零点;
当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ,
,
单调递减区间为![]() ,
,![]() ,
,
当![]() 时,即
时,即![]() 时,函数有两个零点;
时,函数有两个零点;
![]() 时,仅有一个零点;
时,仅有一个零点;![]() ,函数无零点,故③错误;
,函数无零点,故③错误;
当![]() 时,函数在
时,函数在![]() 上单调递增,则
上单调递增,则![]() ,
,
解得![]() ,显然不成立;
,显然不成立;
当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ,
,
当![]() 时,即
时,即![]() ,
,![]() ,解得
,解得![]() ,成立;
,成立;
当![]() ,即
,即![]() ,
,![]() ,解得
,解得![]() ,显然不成立,
,显然不成立,
故④正确;
故答案为:②④


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】有2013位来自不同国家的代表参加一个会议,每位代表都懂得若干种语言,已知其中任意四位代表之间都可进行交谈而不需要此四位代表以外的其他人帮助,即此四人中的任意两人都能讲同一种语言而实现直接沟通,或者通过第三个人的翻译实现间接沟通,或者通过他们各自的翻译能讲的同一种语言实现低效的间接沟通,证明:可以将所有代表分配住进671个房间,每个房间住3人,使得每个房间的3人都可以交谈。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市移动公司为了提高服务质量,决定对使用A,B两种套餐的集团用户进行调查,准备从本市![]() 个人数超过1000人的大集团和8个人数低于200人的小集团中随机抽取若干个集团进行调查,若一次抽取2个集团,全是小集团的概率为
个人数超过1000人的大集团和8个人数低于200人的小集团中随机抽取若干个集团进行调查,若一次抽取2个集团,全是小集团的概率为![]() .
.
![]() 求n的值;
求n的值;
![]() 若取出的2个集团是同一类集团,求全为大集团的概率;
若取出的2个集团是同一类集团,求全为大集团的概率;
![]() 若一次抽取4个集团,假设取出小集团的个数为X,求X的分布列和期望.
若一次抽取4个集团,假设取出小集团的个数为X,求X的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的参数方程为
的参数方程为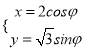 (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求经过椭圆![]() 右焦点
右焦点![]() 且与直线
且与直线![]() 垂直的直线的极坐标方程;
垂直的直线的极坐标方程;
(2)若![]() 为椭圆
为椭圆![]() 上任意-点,当点
上任意-点,当点![]() 到直线
到直线![]() 距离最小时,求点
距离最小时,求点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆周上有![]() 个白点,先将其中一个染为黑色(称为第一次染色),对任何正整数
个白点,先将其中一个染为黑色(称为第一次染色),对任何正整数![]() ,第
,第![]() 次染色后按逆时针方向间隔
次染色后按逆时针方向间隔![]() 个点将下个点染成与原来颜色相反的颜色(称为第
个点将下个点染成与原来颜色相反的颜色(称为第![]() 次染色).
次染色).
(1)对给定正整数![]() ,是否存在正整数
,是否存在正整数![]() ,使
,使![]() 次染色后
次染色后![]() 个点均为白色?
个点均为白色?
(2)对给定正整数![]() ,是否存在正整数
,是否存在正整数![]() ,使
,使![]() 次染色后
次染色后![]() 个点均为黑色?
个点均为黑色?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com