
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)若函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求
,求![]() 的值;
的值;
(Ⅱ)当![]() 时,若不等式
时,若不等式![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(Ⅲ)当![]() 时,若方程
时,若方程![]() 在
在![]() 上总有两个不等的实根, 求
上总有两个不等的实根, 求![]() 的最小值.
的最小值.
【答案】(1)![]() ,
,![]() . (2)
. (2)![]() (3)
(3)![]()
【解析】试题分析:(1)根据导数的几何意义得到参数值;(2)不等式![]() 恒成立,即
恒成立,即![]() ,
,
等价于![]() ,令
,令![]() ,对这个函数求导研究单调性求最值即可;(3)
,对这个函数求导研究单调性求最值即可;(3)![]() 即
即![]() ,
,![]() ,令
,令![]() ,对这个函数求导研究函数的单调性,求得函数的变化趋势,使得函数和x轴有两个不同的交点即可.
,对这个函数求导研究函数的单调性,求得函数的变化趋势,使得函数和x轴有两个不同的交点即可.
解析:(Ⅰ) ![]() ,
,![]() .
.
(Ⅱ)当![]() 时,
时,![]() .
. ![]() (
(![]() ).所以
).所以![]() 即
即![]() .
.
又因为![]() ,所以
,所以![]() 等价于
等价于![]() .
.
令![]() ,则
,则![]() .解
.解![]() ,得
,得![]() ;解
;解![]() ,得
,得![]() ;解
;解![]() ,得
,得![]() .
.
所以![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,所以
单调递减,所以![]() ,
,
故实数![]() 的取值范围是
的取值范围是![]()
(Ⅲ)当![]() 时,
时,![]() 即
即![]() ,
,![]() .
.
令![]() ,则
,则![]() .
.
方程![]() 在
在![]() 上总有两个不等的实根等价于
上总有两个不等的实根等价于
函数![]() 的图象与
的图象与![]() 轴在
轴在![]() 上有两个不同的交点.
上有两个不同的交点.
(ⅰ)当![]() 时,因为
时,因为![]() ,所以
,所以![]() ,所以函数
,所以函数![]() 在
在![]() 单调递减,
单调递减,
从而函数![]() 在
在![]() 内的零点最多一个,不符合题意.
内的零点最多一个,不符合题意.
(ⅱ)当![]() 时,因为
时,因为![]() ,
,
解![]() ,得
,得![]() ;解
;解![]() ,得
,得![]() ;解
;解![]() ,得
,得![]() .
.
所以函数![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
![]() 当
当![]() 时,
时,![]() 在
在![]() 单调递减,函数
单调递减,函数![]() 在区间
在区间![]() 内的零点最多一个,不符
内的零点最多一个,不符
②当![]() 时,因为当
时,因为当![]() 趋于
趋于![]() 时,
时,![]() 的值趋于正无穷大,
的值趋于正无穷大,
所以当且仅当![]() 时函数
时函数![]() 在
在![]() 有两个零点.
有两个零点.
由![]() 得
得![]() ,即
,即![]() 对
对![]() 恒成立. 等价于
恒成立. 等价于![]() .
.
再令![]() ,则
,则![]() .
.
解![]() 得
得![]() ;解
;解![]() 得
得![]() ;解
;解![]() 得
得![]() .
.
所以函数![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减.
单调递减.
所以![]() ,故
,故![]() 的解为
的解为![]() .
.
由![]() 得
得![]() 即
即![]() 对
对![]() 恒成立.所以
恒成立.所以![]() ,
,
所以![]() 的解为
的解为![]() .所以
.所以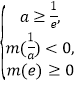 的解为
的解为![]() . 综合①②得
. 综合①②得![]() .
.
综合(ⅰ)(ⅱ)得满足题意要求的实数![]() 的最小值为
的最小值为![]() .
.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:
【题目】已知 ![]() ,方程f(x)=0有3个不同的根.
,方程f(x)=0有3个不同的根.
(1)求实数m的取值范围;
(2)是否存在实数m,使得f(x)在(0,1)上恰有两个极值点x1 , x2且满足x2=2x1 , 若存在,求实数m的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据条件,求下列曲线的方程.
(1)已知两定点![]() ,曲线上的点
,曲线上的点![]() 到
到![]() 距离之差的绝对值为
距离之差的绝对值为![]() ,求曲线的方程;
,求曲线的方程;
(2)在 ![]() 轴上的一个焦点与短轴两端点的连线互相垂直,且焦距为
轴上的一个焦点与短轴两端点的连线互相垂直,且焦距为![]() 的椭圆的标准方程.
的椭圆的标准方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)已知点![]() 为抛物线
为抛物线![]() 的焦点,点
的焦点,点![]() 在抛物线
在抛物线![]() 上,且
上,且![]() .
.

(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)已知点![]() ,延长
,延长![]() 交抛物线
交抛物线![]() 于点
于点![]() ,证明:以点
,证明:以点![]() 为圆心且与直线
为圆心且与直线![]() 相切的圆,必与直线
相切的圆,必与直线![]() 相切.
相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明一家订阅的晚报会在下午5:30~6:30之间的任何一个时间随机地被送到,小明一家人在下午6:00~7:00之间的任何一个时间随机地开始晚餐.
(1)你认为晚报在晚餐开始之前被送到和晚餐开始之后被送到哪一种可能性更大?
(2)晚报在晚餐开始之前被送到的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,点
两点,点![]() 的坐标为
的坐标为![]() ,当
,当![]() 变化时,解答下列问题:
变化时,解答下列问题:
(![]() )能否出现
)能否出现![]() 的情况?说明理由.
的情况?说明理由.
(![]() )证明过
)证明过![]() ,
,![]() ,
,![]() 三点的圆在
三点的圆在![]() 轴上截得的弦长为定值.
轴上截得的弦长为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn , 且S2=11,S5=50,则过点P(n,an)和Q(n+2,an+2)(n∈N*)的直线的一个方向向量的坐标可以是( )
A.(﹣1,﹣3)
B.(1,﹣3)
C.(1,1)
D.(1,﹣1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() (
(![]() ,且
,且![]() ,
,![]() )是定义在区间
)是定义在区间![]() 上的奇函数,
上的奇函数,
(1)求![]() 的值和实数
的值和实数![]() 的值;
的值;
(2)判断函数![]() 在区间
在区间![]() 上的单调性,并说明理由;
上的单调性,并说明理由;
(3)若![]() 且
且![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com