【题目】在平面上， 
⊥ 
，| 
|=| 
|=1， 
= + ．若| 
|＜ 
，则| 
|的取值范围是（ ）
A.（0， 
]
B.（ ， 
]
C.（ ， 
]
D.（ ， ]
【答案】D
【解析】解：根据条件知A，B1 ， P，B2构成一个矩形AB1PB2 ， 以AB1 ， AB2所在直线为坐标轴建立直角坐标系，设|AB1|=a，|AB2|=b，点O的坐标为（x，y），则点P的坐标为（a，b），
由| 
|=| 
|=1，得 
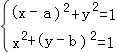，则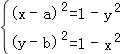 
∵| 
|＜ 
，∴ 
∴ 
∴ 
∵（x﹣a）2+y2=1，∴y2=1﹣（x﹣a）2≤1，
∴y2≤1
同理x2≤1
∴x2+y2≤2②
由①②知 
，
∵| 
|= 
，∴ 
＜| |≤ 
故选D．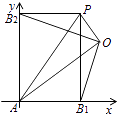
【考点精析】利用平面向量的基本定理及其意义对题目进行判断即可得到答案，需要熟知如果
、
是同一平面内的两个不共线向量，那么对于这一平面内的任意向量
，有且只有一对实数
、
，使
．
每日10分钟口算心算速算天天练系列答案科目：高中数学 来源： 题型：
【题目】有两位射击运动员在一次射击测试中各射靶7次，每次命中的环数如下：
甲 7 8 10 9 8 8 6 乙 9 10 7 8 7 7 8
则下列判断正确的是（ ）
A. 甲射击的平均成绩比乙好 B. 甲射击的成绩的众数小于乙射击的成绩的众数
C. 乙射击的平均成绩比甲好 D. 甲射击的成绩的极差大于乙射击的成绩的极差
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】国家边防安全条例规定：当外轮与我国海岸线的距离小于或等于
海里时，就会被警告.如图，设
，
是海岸线上距离
海里的两个观察站，满足
，一艘外轮在
点满足
，
.
（1）
，
满足什么关系时，就该向外轮发出警告令其退出我国海域？
（2）当
时，间处于什么范围内可以避免使外轮进入被警告区域？
查看答案和解析>>
科目：高中数学 来源： 题型：
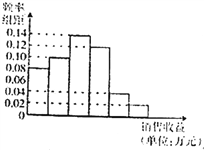
【题目】某公司为了解广告投入对销售收益的影响，在若干地区各投入
万元广告费用，并将各地的销售收益（单位：万元）绘制成如图所示的频率分布直方图.由于工作人员操作失误，横轴的数据丢失，但可以确定横轴是从
开始计数的.
广告投入 | 1 | 2 | 3 | 4 | 5 |
销售收益 | 2 | 3 | 2 | 5 | 7 |
（Ⅰ）根据频率分布直方图计算图中各小长方形的宽度；
（Ⅱ）该公司按照类似的研究方法，测得另外一些数据，并整理得到上表：
表中的数据显示
与
之间存在线性相关关系，求关于的回归方程；
（Ⅲ）若广告投入
万元时，实际销售收益为
万元，求残差
.
附：
，
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，曲线
是一条居民平时散步的小道，小道两旁是空地，当地政府为了丰富居民的业余生活，要在小道两旁规划出两地来修建休闲活动场所，已知空地
和规划的两块用地（阴影区域）都是矩形，
，
，
，若以
所在直线为
轴，
为原点，建立如图平面直角坐标系，则曲线的方程为
，记
，规划的两块用地的面积之和为
.（单位：）
（1）求关于
的函数
；
（2）求的最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，四棱锥P﹣ABCD中，PA⊥底面ABCD，BC=CD=2，AC=4，∠ACB=∠ACD= 
，F为PC的中点，AF⊥PB． 
（1）求PA的长；
（2）求二面角B﹣AF﹣D的正弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】据监测，在海滨某城市附近的海面有一台风. 台风中心位于城市
的东偏南
方向、距离城市
的海面
处，并以
的速度向西偏北
方向移动（如图示）.如果台风侵袭范围为圆形区域，半径
，台风移动的方向与速度不变，那么该城市受台风侵袭的时长为_____ .
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】【2018河南安阳市高三一模】如下图，在平面直角坐标系
中，直线
与直线
之间的阴影部分即为
，区域
中动点
到
的距离之积为1．
（Ⅰ）求点
的轨迹
的方程；
（Ⅱ）动直线
穿过区域
，分别交直线
于
两点，若直线
与轨迹
有且只有一个公共点，求证： 
的面积恒为定值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
