
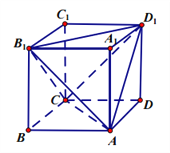
【题目】在棱长为2的正方体![]() 中.
中.
(1)求几何体![]() 的表面积;
的表面积;
(2)若![]() 分别是棱
分别是棱![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() .
.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:(1)先证明几何体![]() 是每个面都是正三角形的四面体,再利用正三角形面积公式可得结果;(2)取
是每个面都是正三角形的四面体,再利用正三角形面积公式可得结果;(2)取![]() 的中点
的中点![]() ,连
,连![]() ,根据三角形中位线定理可证明四边形
,根据三角形中位线定理可证明四边形![]() 为平行四边形,从而可得
为平行四边形,从而可得![]() ,再根据线面平行的判定定理即可证明
,再根据线面平行的判定定理即可证明![]() 平面
平面![]() .
.
试题解析:(1)∵![]() 是棱长为2的正方体,
是棱长为2的正方体,
所以![]() ,故几何体
,故几何体![]() 是每个面都是正三角形的四面体,三角形
是每个面都是正三角形的四面体,三角形![]() 的面积是
的面积是![]() ,所以几何体
,所以几何体![]() 的表面积是
的表面积是![]() .
.
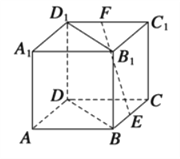
(2)法一:证明:取![]() 的中点
的中点![]() ,连
,连![]() ,
,
∵![]() ,
, ![]() ,
,
∵![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
,
∴四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,
,
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
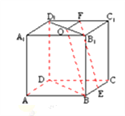
法二
证明:取B1C1的中点M,连接ME,MF,
在△D1B1C1中,MF分别是边B1C1,D1C1的中点,
∴MF∥D1B1,又![]() 平面DBB1D1,D1B1
平面DBB1D1,D1B1![]() 平面DBB1D1,
平面DBB1D1,
∴MF∥平面DBB1D1,
在正方形BCC1B1中,∵ME是对边B1C1,BC的中点,∴BE∥B1M,BE=B1M,
∴四边形BEMB1是平行四边形,所以ME∥BB1,
又![]() 平面DBB1D1,BB1
平面DBB1D1,BB1![]() 平面DBB1D1,
平面DBB1D1,
∴ME∥平面DBB1D1,又![]()
所以平面MEF∥平面DBB1D1,且![]() 平面MEF
平面MEF
所以EF∥平面DBB1D1,

【方法点晴】本题主要考查线面平行的判定定理以及三棱锥的表面积,属于难题. 证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面. 本题(2)是就是利用方法①证明的.


科目:高中数学 来源: 题型:
【题目】某火锅店为了解气温对营业额的影响,随机记录了该店1月份中5天的日营业额y(单位:千元)与该地当日最低气温x(单位:℃)的数据,如表:
x | 2 | 8 | 9 | 11 | 5 |
y | 12 | 8 | 8 | 7 | 10 |
(1)求y关于x的回归方程 ![]() ;
;
(2)判定y与x之间是正相关还是负相关;若该地1月份某天的最低气温为6℃,用所求回归方程预测该店当日的营业额. (附:回归方程 ![]() 中,
中, ![]() =
= 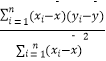 =
= 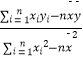 ,
, ![]() =
= ![]() ﹣
﹣ ![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l经过直线2x+y-5=0与x-2y=0的交点P.
(1)点A(5,0)到直线l的距离为3,求直线l的方程;
(2)求点A(5,0)到直线l的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在二项式( ![]() +
+ ![]() )n展开式中,前三项的系数成等差数列. 求:(1)展开式中各项系数和;
)n展开式中,前三项的系数成等差数列. 求:(1)展开式中各项系数和;
【答案】解:由题意得2 ![]() ×
× ![]() =1+
=1+ ![]() ×
× ![]() ,
,
化为:n2﹣9n+8=0,解得n=1(舍去)或8.
∴n=8.
在 ![]() 中,令x=1,可得展开式中各项系数和=
中,令x=1,可得展开式中各项系数和= ![]() =
= ![]() .
.
(1)展开式中系数最大的项.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD-A1B1C1D1中,下列说法正确的是____ (填序号).
(1)直线AC1在平面CC1B1B内.
(2)设正方形ABCD与A1B1C1D1的中心分别为O、O1,则平面AA1C1C与平面BB1D1D的交线为OO1.
(3)由A、C1、B1确定的平面是ADC1B1.
(4)由A、C1、B1确定的平面与由A、C1、D确定的平面是同一个平面.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设复数z=2m+(4-m2)i,当实数m取何值时,复数z对应的点:
(1)位于虚轴上?
(2)位于一、三象限?
(3)位于以原点为圆心,以4为半径的圆上?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中有20个大小相同的球,其中记上0号的有10个,记上n号的有n个(n=1,2,3,4),现从袋中任取一球,X表示所取球的标号.
(1)求X的分布列,均值和方差;
(2)若Y=aX+b,E(Y)=1,D(Y)=11,试求a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设F为双曲线 ![]() ﹣
﹣ ![]() =1(a>b>0)的右焦点,过点F的直线分别交两条渐近线于A,B两点,OA⊥AB,若2|AB|=|OA|+|OB|,则该双曲线的离心率为( )
=1(a>b>0)的右焦点,过点F的直线分别交两条渐近线于A,B两点,OA⊥AB,若2|AB|=|OA|+|OB|,则该双曲线的离心率为( ) 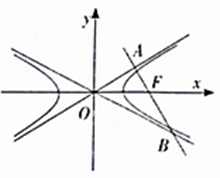
A.![]()
B.2
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com