
【题目】已知圆C经过点A(﹣2,0),B(0,2),且圆心C在直线y=x上,又直线l:y=kx+1与圆C相交于P、Q两点.
(1)求圆C的方程;
(2)若 ![]() =﹣2,求实数k的值;
=﹣2,求实数k的值;
(3)过点(0,4)作动直线m交圆C于E,F两点.试问:在以EF为直径的所有圆中,是否存在这样的圆P,使得圆P经过点M(2,0)?若存在,求出圆P的方程;若不存在,请说明理由.
【答案】
(1)解:设圆心C(a,a),半径为r.
因为圆C经过点A(﹣2,0),B(0,2),
所以|AC|=|BC|=r,
即 ![]() ,
,
解得a=0,r=2,
所以圆C的方程是x2+y2=4
(2)解:因为 ![]() =2×2×cos<
=2×2×cos< ![]() >=﹣2,
>=﹣2,
且 ![]() 与
与 ![]() 的夹角为∠POQ,
的夹角为∠POQ,
所以cos∠POQ=﹣ ![]() ,∠POQ=120°,
,∠POQ=120°,
所以圆心C到直线l:kx﹣y+1=0的距离d=1,
又d= ![]() ,所以k=0
,所以k=0
(3)解:(ⅰ)当直线m的斜率不存在时,
直线m经过圆C的圆心C,
此时直线m与圆C的交点为E(0,2),F(0,﹣2),
EF即为圆C的直径,而点M(2,0)在圆C上,
即圆C也是满足题意的圆.
(ⅱ)当直线m的斜率存在时,设直线m:y=kx+4,
由 ![]() ,消去y整理,得(1+k2)x2+8kx+12=0,
,消去y整理,得(1+k2)x2+8kx+12=0,
由△=64k2﹣48(1+k2)>0,得 ![]() 或
或 ![]() .
.
设E(x1,y1),F(x2,y2),
则有 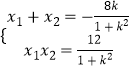 ①
①
由①得 ![]() ,②
,② ![]() ,③
,③
若存在以EF为直径的圆P经过点M(2,0),则ME⊥MF,
所以 ![]() ,
,
因此(x1﹣2)(x2﹣2)+y1y2=0,
即x1x2﹣2(x1+x2)+4+y1y2=0,)
则 ![]() ,
,
所以16k+32=0,k=﹣2,满足题意.
此时以EF为直径的圆的方程为x2+y2﹣(x1+x2)x﹣(y1+y2)y+x1x2+y1y2=0,
即 ![]() ,
,
亦即5x2+5y2﹣16x﹣8y+12=0.
综上,在以EF为直径的所有圆中,
存在圆P:5x2+5y2﹣16x﹣8y+12=0或x2+y2=4,使得圆P经过点M(2,0)
【解析】(1)设圆心C(a,a),半径为r.|AC|=|BC|=r,由此能求出圆C的方程.(2)由 ![]() =2×2×cos<
=2×2×cos< ![]() >=﹣2,得∠POQ=120°,圆心C到直线l:kx﹣y+1=0的距离d=1,由此能求出k=0.(3)当直线m的斜率不存在时,圆C也是满足题意的圆;当直线m的斜率存在时,设直线m:y=kx+4,由
>=﹣2,得∠POQ=120°,圆心C到直线l:kx﹣y+1=0的距离d=1,由此能求出k=0.(3)当直线m的斜率不存在时,圆C也是满足题意的圆;当直线m的斜率存在时,设直线m:y=kx+4,由 ![]() ,得(1+k2)x2+8kx+12=0,由此利用根的判别式、韦达定理,结合已知条件能求出在以EF为直径的所有圆中,存在圆P:5x2+5y2﹣16x﹣8y+12=0或x2+y2=4,使得圆P经过点M(2,0).
,得(1+k2)x2+8kx+12=0,由此利用根的判别式、韦达定理,结合已知条件能求出在以EF为直径的所有圆中,存在圆P:5x2+5y2﹣16x﹣8y+12=0或x2+y2=4,使得圆P经过点M(2,0).


科目:高中数学 来源: 题型:
【题目】滨湖区拟建一主题游戏园,该游戏园为四边形区域ABCD,其中三角形区城ABC为主题活动区,其中∠ACB=60°,∠ABC=45°,AB=12 ![]() m;AD、CD为游客通道(不考虑宽度),且∠ADC=120°,通道AD、CD围成三角形区域ADC为游客休闲中心,供游客休憩.
m;AD、CD为游客通道(不考虑宽度),且∠ADC=120°,通道AD、CD围成三角形区域ADC为游客休闲中心,供游客休憩. 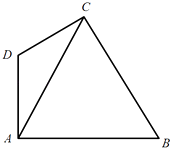
(1)求AC的长度;
(2)记游客通道AD与CD的长度和为L,求L的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产某种水杯,每个水杯的原材料费、加工费分别为30元、m元(m为常数,且2≤m≤3),设每个水杯的出厂价为x元(35≤x≤41),根据市场调查,水杯的日销售量与ex(e为自然对数的底数)成反比例,已知每个水杯的出厂价为40元时,日销售量为10个.
(1)求该工厂的日利润y(元)与每个水杯的出厂价x(元)的函数关系式;
(2)当每个水杯的出厂价为多少元时,该工厂的日利润最大,并求日利润的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一次猜奖游戏中,1,2,3,4四扇门里摆放了![]() ,
, ![]() ,
, ![]() ,
, ![]() 四件奖品(每扇门里仅放一件).甲同学说:1号门里是
四件奖品(每扇门里仅放一件).甲同学说:1号门里是![]() ,3号门里是
,3号门里是![]() ;乙同学说:2号门里是
;乙同学说:2号门里是![]() ,3号门里是
,3号门里是![]() ;丙同学说:4号门里是
;丙同学说:4号门里是![]() ,2号门里是
,2号门里是![]() ;丁同学说:4号门里是
;丁同学说:4号门里是![]() ,3号门里是
,3号门里是![]() .如果他们每人都猜对了一半,那么4号门里是( )
.如果他们每人都猜对了一半,那么4号门里是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是首项为a1= ![]() ,公比q=
,公比q= ![]() 的等比数列,设bn+2=3
的等比数列,设bn+2=3 ![]() an(n∈N*),数列{cn}满足cn=anbn .
an(n∈N*),数列{cn}满足cn=anbn .
(1)求证:{bn}是等差数列;
(2)求数列{cn}的前n项和Sn;
(3)若cn≤ ![]() +m﹣1对一切正整数n恒成立,求实数m的取值范围.
+m﹣1对一切正整数n恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85,乙班学生成绩的中位数是83,则x+y的值为 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】电视台播放甲、乙两套连续剧,每次播放连续剧时,需要播放广告.已知每次播放甲、乙两套连续剧时,连续剧播放时长、广告播放时长、收视人次如下表所示:
连续剧播放时长(分钟) | 广告播放时长(分钟) | 收视人次(万) | |
甲 | 70 | 5 | 60 |
乙 | 60 | 5 | 25 |
已知电视台每周安排的甲、乙连续剧的总播放时间不多于600分钟,广告的总播放时间不少于30分钟,且甲连续剧播放的次数不多于乙连续剧播放次数的2倍.分别用![]() ,
,![]() 表示每周计划播出的甲、乙两套连续剧的次数.
表示每周计划播出的甲、乙两套连续剧的次数.
(1)用![]() ,
,![]() 列出满足题目条件的数学关系式,并画出相应的平面区域;
列出满足题目条件的数学关系式,并画出相应的平面区域;
(2)问电视台每周播出甲、乙两套连续剧各多少次,才能使收视人次最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面内三个向量: ![]() =(3,2),
=(3,2), ![]() =(﹣1,2),
=(﹣1,2), ![]() =(4,1)
=(4,1)
(1)若( ![]() +k
+k ![]() )∥(2
)∥(2 ![]() ﹣
﹣ ![]() ),求实数k的值;
),求实数k的值;
(2)设 ![]() =(x,y),且满足(
=(x,y),且满足( ![]() +
+ ![]() )⊥(
)⊥( ![]() ﹣
﹣ ![]() ),|
),| ![]() ﹣
﹣ ![]() |=
|= ![]() ,求
,求 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴,并在两种坐标系中取相同的长度单位,已知直线
轴正半轴为极轴,并在两种坐标系中取相同的长度单位,已知直线![]() 的参数方程为
的参数方程为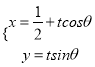 ,(
,( ![]() 为参数,
为参数, ![]() ),曲线
),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
, ![]() 两点,当
两点,当![]() 变化时,求
变化时,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com