
【题目】已知函数![]() .
.
(1)求![]() 的单调区间;
的单调区间;
(2)若![]() ,求证:函数
,求证:函数![]() 只有一个零点
只有一个零点![]() ,且
,且![]() .
.
【答案】(Ⅰ)函数![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() 和
和![]() 当
当![]() 时,
时,![]() . 所以,函数
. 所以,函数![]() 的单调递减区间是
的单调递减区间是![]() 当
当![]() 时,
时,![]() ,函数
,函数![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() 和
和![]() ;(Ⅱ)证明见解析
;(Ⅱ)证明见解析
【解析】
试题(Ⅰ)先求出函数![]() 的定义域,求出函数
的定义域,求出函数![]() 的导数
的导数![]() ,再令
,再令![]() ,求得解,
,求得解,
讨论当![]() 时及
时及![]() ,列出函数
,列出函数![]() 与
与![]() 随
随![]() 的变化情况得到函数的单调区间
的变化情况得到函数的单调区间
(Ⅱ)当![]() 时,由(Ⅰ)知,函数
时,由(Ⅰ)知,函数![]() 的极小值,极大值,并且极小值与极大值均大于0,又由函数
的极小值,极大值,并且极小值与极大值均大于0,又由函数![]() 在
在![]() 是减函数,可得
是减函数,可得![]() 至多有一个零点,又由
至多有一个零点,又由![]() 可得函数
可得函数![]() 只有一个零点,且
只有一个零点,且![]() ,得到证明
,得到证明
试题解析:(Ⅰ)解:![]() 的定义域为
的定义域为![]() .
.![]()
令![]() ,
,![]() 或
或![]()
当![]() 时,
时,![]() ,函数
,函数![]() 与
与![]() 随
随![]() 的变化情况如下表:
的变化情况如下表:
所以,函数![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() 和
和![]()
当![]() 时,
时,![]() . 所以,函数
. 所以,函数![]() 的单调递减区间是
的单调递减区间是![]()
当![]() 时,
时,![]() ,函数
,函数![]() 与
与![]() 随
随![]() 的变化情况如下表:
的变化情况如下表:
所以,函数![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() 和
和![]() .
.
(Ⅱ)证明:当![]() 时,由(Ⅰ)知,
时,由(Ⅰ)知,![]() 的极小值为
的极小值为![]() ,极大值为
,极大值为![]() .
.
因为![]() ,
,![]() 且又由函数
且又由函数![]() 在
在![]() 是减函数,可得
是减函数,可得![]() 至多有一个零点. 又因为
至多有一个零点. 又因为![]() ,所以 函数
,所以 函数![]() 只有一个零点
只有一个零点![]() ,且
,且![]() .
.


科目:高中数学 来源: 题型:
【题目】如图![]() ,在梯形
,在梯形![]() 中,
中, ![]() 于
于![]() ,
, ![]()
![]() .将
.将![]() 沿
沿![]() 折起至
折起至![]() ,使得平面
,使得平面![]() 平面
平面![]() (如图2),
(如图2), ![]() 为线段
为线段![]() 上一点.
上一点.
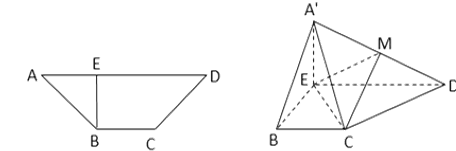
图1 图2
(Ⅰ)求证: ![]() ;
;
(Ⅱ)若![]() 为线段
为线段![]() 中点,求多面体
中点,求多面体![]() 与多面体
与多面体![]() 的体积之比;
的体积之比;
(Ⅲ)是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的长.若不存在,请说明理由.
的长.若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学导师计划从自己所培养的研究生甲、乙两人中选一人,参加雄安新区某部门组织的计算机技能大赛,两人以往5次的比赛成绩统计如下:(满分100分,单位:分).
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
甲的成绩 | 87 | 87 | 84 | 100 | 92 |
乙的成绩 | 100 | 80 | 85 | 95 | 90 |
(1)试比较甲、乙二人谁的成绩更稳定;
(2)在一次考试中若两人成绩之差的绝对值不大于2,则称两人“实力相当”.若从上述5次成绩中任意抽取2次,求恰有一次两人“实力相当”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为椭圆
为椭圆![]() 上任一点,
上任一点, ![]() 为其右焦点,
为其右焦点, ![]() 是椭圆的左、右顶点,点
是椭圆的左、右顶点,点![]() 满足
满足![]() .
.
①证明: ![]() 为定值;
为定值;
②设![]() 是直线
是直线![]() 上的任一点,直线
上的任一点,直线![]() 分别另交椭圆
分别另交椭圆![]() 于
于![]() 两点,求
两点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】—般地,若函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ,则称
,则称![]() 为
为![]() 的“
的“![]() 倍跟随区间”;特别地,若函数
倍跟随区间”;特别地,若函数![]() 的定义域为
的定义域为![]() ,值域也为
,值域也为![]() ,则称
,则称![]() 为
为![]() 的“跟随区间”.下列结论正确的是( )
的“跟随区间”.下列结论正确的是( )
A.若![]() 为
为![]() 的跟随区间,则
的跟随区间,则![]()
B.函数![]() 不存在跟随区间
不存在跟随区间
C.若函数![]() 存在跟随区间,则
存在跟随区间,则![]()
D.二次函数![]() 存在“3倍跟随区间”
存在“3倍跟随区间”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 和椭圆
和椭圆![]() ,
, ![]() 是椭圆
是椭圆![]() 的左焦点.
的左焦点.
(Ⅰ)求椭圆![]() 的离心率和点
的离心率和点![]() 的坐标;
的坐标;
(Ⅱ)点![]() 在椭圆
在椭圆![]() 上,过
上,过![]() 作
作![]() 轴的垂线,交圆
轴的垂线,交圆![]() 于点
于点![]() (
(![]() 不重合),
不重合),![]() 是过点
是过点![]() 的圆
的圆![]() 的切线.圆
的切线.圆![]() 的圆心为点
的圆心为点![]() ,半径长为
,半径长为![]() .试判断直线
.试判断直线![]() 与圆
与圆![]() 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】食品安全问题越来越引起人们的重视,农药、化肥的滥用给人民群众的健康带来了一定的危害.为了给消费者带来放心的蔬菜,某农村合作社每年投入资金![]() 万元,搭建甲、乙两个无公害蔬菜大棚,每个大棚至少要投入资金
万元,搭建甲、乙两个无公害蔬菜大棚,每个大棚至少要投入资金![]() 万元,其中甲大棚种西红柿,乙大棚种黄瓜.根据以往的种菜经验,发现种西红柿的年收入
万元,其中甲大棚种西红柿,乙大棚种黄瓜.根据以往的种菜经验,发现种西红柿的年收入![]() 、种黄瓜的年收入
、种黄瓜的年收入![]() 与各自的资金投入
与各自的资金投入![]() (单位:万元)满足
(单位:万元)满足![]() ,
,![]() .设甲大棚的资金投入为
.设甲大棚的资金投入为![]() (单位:万元),每年两个大棚的总收入为
(单位:万元),每年两个大棚的总收入为![]() (单位:万元).
(单位:万元).
(1)求![]() 的值;
的值;
(2)试问如何安排甲、乙两个大棚的资金投入,才能使总收入![]() 最大.
最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列说法
①互斥事件不一定是对立事件,对立事件一定是互斥事件
②演绎推理是从特殊到一般的推理,它的一般模式是“三段论”
③残差图的带状区域的宽度越窄,说明模型拟合精度越高,回归方程的预报精度越高
④若![]() ,则事件
,则事件![]() 与
与![]() 互斥且对立
互斥且对立
⑤甲乙两艘轮船都要在某个泊位停靠4小时,假定它们在一昼夜的时间段中随机到达,则这两艘船中至少有一艘在停靠泊位时必须等待的概率为![]() .
.
其中正确的说法是______(写出全部正确说法的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com