
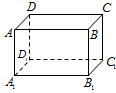
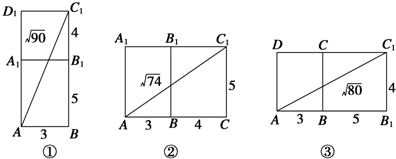
 如图,已知长方体AC1的长、宽、高分别为5、4、3,现有一甲壳虫从A点出发沿长方体表面爬到C1处获取食物,它爬行路线的路程最小值为
如图,已知长方体AC1的长、宽、高分别为5、4、3,现有一甲壳虫从A点出发沿长方体表面爬到C1处获取食物,它爬行路线的路程最小值为| 90 |
| 74 |
| 80 |
| 74 |
| 74 |


科目:高中数学 来源: 题型:
 某网店经营的一红消费品的进价为每件12元,周销售量p(件)与销售价格x(元)的关系,如图中折线所示,每周各项开支合计为20元.
某网店经营的一红消费品的进价为每件12元,周销售量p(件)与销售价格x(元)的关系,如图中折线所示,每周各项开支合计为20元.查看答案和解析>>
科目:高中数学 来源: 题型:
| A、垂直于同一直线的两条直线互相平行 |
| B、平行四边形在一个平面上的平行投影一定是平行四边形 |
| C、平面截正方体所得的截面图形可能是正六边形 |
| D、锐角三角形在一个平面上的平行投影不可能是钝角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| AB |
| AC |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、a<b<c |
| B、a<c<b |
| C、b<c<a |
| D、b<a<c |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com