
【题目】如图是某学校高三年级的三个班在一学期内的六次数学测试的平均成绩y关于测试序号x的函数图象,为了容易看出一个班级的成绩变化,将离散的点用虚线连接,根据图象,给出下列结论:
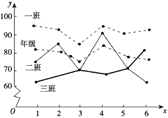
①一班成绩始终高于年级平均水平,整体成绩比较好;
②二班成绩不够稳定,波动程度较大;
③三班成绩虽然多次低于年级平均水平,但在稳步提升.
其中错误的结论的个数为( )
A.0B.1C.2D.3
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,直线
轴的非负半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 与曲线
与曲线![]() 的普通方程;
的普通方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】噪声污染已经成为影响人们身体健康和生活质量的严重问题,为了了解声音强度![]() (单位:分贝)与声音能量(单位:
(单位:分贝)与声音能量(单位:![]() )之间的关系,将测量得到的声音强度
)之间的关系,将测量得到的声音强度![]() 和声音能量
和声音能量![]() (
(![]() =1,2…,10)数据作了初步处理,得到如图散点图及一些统计量的值.
=1,2…,10)数据作了初步处理,得到如图散点图及一些统计量的值.

|
|
|
|
|
| 45.7 |
|
| 0.51 |
|
| |||
| 5.1 | |||
表中![]() ,
,![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个适宜作为声音强度
哪一个适宜作为声音强度![]() 关于声音能量的回归方程类型?(给出判断即可,不必说明理由)
关于声音能量的回归方程类型?(给出判断即可,不必说明理由)
(2)根据表中数据,求声音强度![]() 关于声音能量的回归方程;
关于声音能量的回归方程;
(3)当声音强度大于60分贝时属于噪音,会产生噪音污染,城市中某点![]() 共受到两个声源的影响,这两个声源的声音能量分别是
共受到两个声源的影响,这两个声源的声音能量分别是![]() 和
和![]() ,且
,且![]() .己知点
.己知点![]() 的声音能量等于声音能量
的声音能量等于声音能量![]() 与
与![]() 之和.请根据(1)中的回归方程,判断
之和.请根据(1)中的回归方程,判断![]() 点是否受到噪音污染的干扰,并说明理由.
点是否受到噪音污染的干扰,并说明理由.
附:对于一组数据![]() .其回归直线
.其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: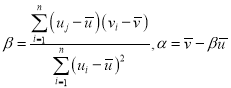 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是偶函数,且当
是偶函数,且当![]() 时,
时,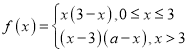
(1)当![]() 时,求
时,求![]() 的解析式;
的解析式;
(2)设函数![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,试求
,试求![]() 的表达式;
的表达式;
(3)若方程![]() 有四个不同的实根,且它们成等差数列,试探求
有四个不同的实根,且它们成等差数列,试探求![]() 与
与![]() 满足的条件.
满足的条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(x+)(A>0,>0,0<<)的部分图象如图所示,又函数g(x)=f(x+![]() ).
).
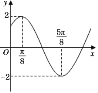
(1)求函数g(x)的单调增区间;
(2)设![]() ABC的内角ABC的对边分别为abc,又c=
ABC的内角ABC的对边分别为abc,又c=![]() ,且锐角C满足g(C)= -1,若sinB=2sinA,,求ABC的面积.
,且锐角C满足g(C)= -1,若sinB=2sinA,,求ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,直线
轴的非负半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的极坐标方程和直线
的极坐标方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)若射线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,与直线
两点,与直线![]() 交于
交于![]() 点,射线
点,射线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com