
| A. | 充分不必要条件 | B. | 充分必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分又不必要条件 |
分析 由“$\frac{{f({x_1})-f({x_2})}}{{{x_1}-{x_2}}}>0$”?(x1-x2)[f(x1)-f(x2)]>0,?x1-x2与f(x1)-f(x2)同号.利用增函数的定义即可判断出结论.
解答 解:“$\frac{{f({x_1})-f({x_2})}}{{{x_1}-{x_2}}}>0$”?(x1-x2)[f(x1)-f(x2)]>0,?x1-x2与f(x1)-f(x2)同号.
∴对于任意的x1,x2∈(m,n)且x1≠x2,则“f(x)是(m,n)上的增函数”是“$\frac{{f({x_1})-f({x_2})}}{{{x_1}-{x_2}}}>0$”的充要条件.
故选:B.
点评 本题考查了不等式的解法、充要条件的判定方法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
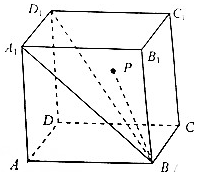 在正方体ABCD-A1B1C1D1中,点P在CDD1C1所在的平面上,满足∠PBD1=∠A1BD1,则动点P的轨迹是( )
在正方体ABCD-A1B1C1D1中,点P在CDD1C1所在的平面上,满足∠PBD1=∠A1BD1,则动点P的轨迹是( )| A. | 圆 | B. | 椭圆 | C. | 双曲线 | D. | 抛物线 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{4}$+$\frac{1}{4}$i | D. | $\frac{\sqrt{3}}{4}$-$\frac{1}{4}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | $4\sqrt{3}$ | C. | $\frac{{4\sqrt{3}}}{3}$ | D. | $\frac{32}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com