Question

将一颗质地均匀的正方体骰子（六个面的点数分别为1，2，3，4，5，6）先后抛掷两次，记第一次出现的点数为a，第二次出现的点数为b．设复数z=a+bi．
（1）求事件“z-3i为实数”的概率；
（2）求事件“复数z在复平面内的对应点（a，b）满足（a-2）²+b²≤9”的概率．

Answer 1

解：（1）z-3i为实数，即a+bi-3i=a+（b-3）i为实数，
∴b=3．依题意a可取1，2，3，4，5，6，
故出现b=3的概率为p₁==，
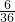
即事件“z-3i为实数”的概率为．
（2）由条件可知，b的值只能取1，2，3．
当b=1时，（a-2）²≤8，即a可取1，2，3，4，
当b=2时，（a-2）²≤5，即a可取1，2，3，4，
当b=3时，（a-2）²≤0，即a可取2．
∴共有9种情况下可使事件发生，又a，b的取值情况共有36种，
所以事件“点（a，b）满足（a-2）²+b²≤9”的概率为
p₂=++=．
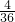
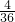
分析：由题意可得（a，b）的所有结果共有36种，每种结果等可能出现
（1）若z-3i为实数，则a+bi-3i=a+（b-3）i为实数，b=3．依题意a可取1，2，3，4，5，6，从而可得符合条件的（a，b）的个数，代入概率的计算公式可求
（2）复数z在复平面内的对应点（a，b）满足（a-2）²+b²≤9，考虑到b的值只能取1，2，3，分别代入b的值，可求对应的a，找出所有符合条件的（a，b）的个数，代入概率的计算公式可求
点评：本题以古典概率的计算为载体，综合考查了分步计数原理，复数的概念，不等式的知识，等可能事件的概率计算，但考查的都是基本概念、基本方法
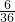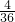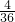