
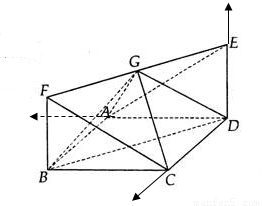
.如图:四边形 为正方形,
为正方形, 为矩形,
为矩形, 平面
平面 ,
,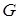 为
为 的中点(Ⅰ)求证
的中点(Ⅰ)求证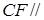 平面
平面 ;(Ⅱ)求证平面
;(Ⅱ)求证平面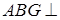 平面
平面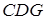 ;
;
(Ⅲ)求二面角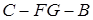 的余弦植。
的余弦植。
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
 (2010•福建模拟)(1)选修4-2:矩阵与变换
(2010•福建模拟)(1)选修4-2:矩阵与变换| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:047
如图所示,设
a=(-l-x)i,b=(1-x)i+yj(x,y∈R,i,j分别是x、y轴正方向上的单位向量),且|a|=|b|.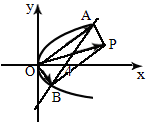
(1)
求点M(x,y)的轨迹C的方程;(2)
过点(4,0)作直线l交曲线C于A、B两点,设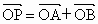 ,求证:四边形OAPB为矩形.
,求证:四边形OAPB为矩形.查看答案和解析>>
科目:高中数学 来源:福建省模拟题 题型:解答题
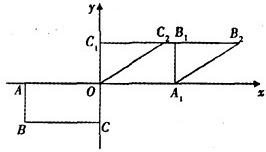
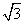 ,1),求此矩形OABC变为平行四边形OA1B2C2的线性变换对应的矩阵.
,1),求此矩形OABC变为平行四边形OA1B2C2的线性变换对应的矩阵. 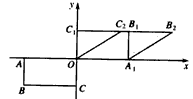
查看答案和解析>>
科目:高中数学 来源: 题型:

图10
查看答案和解析>>
科目:高中数学 来源:2010年福建省普通高中毕业班质量检查数学试卷(理科)(解析版) 题型:解答题
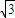 ,1).求将矩形OABC变为平行四边形OA1B2C2的线性变换对应的矩阵.
,1).求将矩形OABC变为平行四边形OA1B2C2的线性变换对应的矩阵.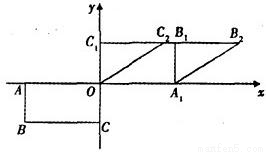
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com