【题目】如果方程cos2x－sinx＋a＝0在(0，
]上有解，求a的取值范围．
【答案】见解析
【解析】方法一 设f(x)＝－cos2x＋sinx(x∈(0，
])．
显然当且仅当a属于f(x)的值域时，a＝f(x)有解．
因为f(x)＝－(1－sin2x)＋sinx
＝(sinx＋
)2－
，
且由x∈(0，]知sinx∈(0,1]．
易求得f(x)的值域为(－1,1]．
故a的取值范围是(－1,1]．
方法二 令t＝sinx，由x∈(0，]，可得t∈(0,1]．
将方程变为t2＋t－1－a＝0.
依题意，该方程在(0,1]上有解．
设f(t)＝t2＋t－1－a.
其图象是开口向上的抛物线，对称轴t＝－，
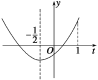
如图所示．
因此f(t)＝0在(0,1]上有解等价于
即
所以－1<a≤1.
故a的取值范围是(－1,1]．
巧学巧练系列答案科目：高中数学 来源： 题型：
【题目】已知在极坐标系中点C的极坐标为
.
(1)求出以点C为圆心，半径为2的圆的极坐标方程(写出解题过程)并画出图形；
(2)在直角坐标系中，以圆C所在极坐标系的极点为原点，极轴为x轴的正半轴建立直角坐标系，点P是圆C上任意一点，Q(5，－
)，M是线段PQ的中点，当点P在圆C上运动时，求点M的轨迹的普通方程．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知
，
∈[1，＋∞).
（1）当
时，判断函数
的单调性并证明；
（2）当时，求函数
的最小值；
（3）若对任意∈[1，＋∞)，＞0恒成立，试求实数
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
，其中
为常数.
（1）若
，求曲线
在点
处的切线方程；
（2）若
，求
零点的个数；
（3）若
为整数，且当
时， 
恒成立，求
的最大值.
（参考数据
， 
， 
）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】现从某班的一次期末考试中，随机的抽取了七位同学的数学(满分150分）、物理（满分110分）成绩如下表所示，数学、物理成绩分别用特征量
表示，
特征量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
t | 101 | 124 | 119 | 106 | 122 | 118 | 115 |
y | 74 | 83 | 87 | 75 | 85 | 87 | 83 |
求
关于t的回归方程；
（2）利用（1）中的回归方程，分析数学成绩的变化对物理成绩的影响，并估计该班某学生数学成绩130分时，他的物理成绩(精确到个位).
附：回归方程
中斜率和截距的最小二乘估计公式分别为：
． 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某公司对新研发的一种产品进行试销，得到如下数据及散点图：
其中
， 
， 
， 
.
（1）根据散点图判断
与
， 
与
哪一对具有较强的线性相关性（给出判断即可，不必说明理由）？
（2）根据（1）的判断结果及数据，建立
关于
的回归方程（运算过程及回归方程中的系数均保留两位有效数字）.
（3）定价为150元/ 
时，天销售额的预报值为多少元？
附：对于一组数据
，其回归直线
的斜率和截距的最小二乘法估计分别为
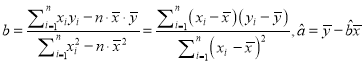
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=x3-3ax+e，g（x）=1-lnx，其中e为自然对数的底数.
（I）若曲线y=f（x）在点（1，f（1））处的切线与直线l：x+2y=0垂直，求实数a的值；
（II）设函数F（x）=-x[g（x）+
x-2]，若F（x）在区间（m,m+1）（m∈Z）内存在唯一的极值点，求m的值；
（III）用max{m，n}表示m，n中的较大者，记函数h（x）=max{f（x），g（x）}（x>0）. 若函数h（x）在（0，+∞）上恰有2个零点，求实数a的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知向量
， 
，设函数
.
（1）求函数
的最小正周期；
（2）已知
分别为三角形
的内角对应的三边长， 
为锐角， 
， 
，且
恰是函数
在
上的最大值，求
和三角形
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
