
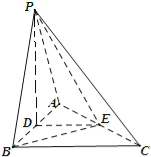
【题目】如图,在三棱锥P﹣ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D,E分别为AB,AC中点.
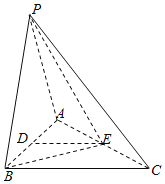
(1)求证:DE∥平面PBC;
(2)求证:AB⊥PE;
(3)求三棱锥P﹣BEC的体积.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】试题分析:(I)根据三角形中位线定理,证出DE∥BC,再由线面平行判定定理即可证出DE∥面PBC;
(II)连结PD,由等腰三角形“三线合一”,证出PD⊥AB,结合DE⊥AB证出AB⊥平面PDE,由此可得AB⊥PE;
(III)由面面垂直性质定理,证出PD⊥平面ABC,得PD是三棱锥P﹣BEC的高.结合题中数据算出PD=![]() 且S△BEC=
且S△BEC=![]() ,利用锥体体积公式求出三棱锥P﹣BEC的体积,即得三棱锥B﹣PEC的体积.
,利用锥体体积公式求出三棱锥P﹣BEC的体积,即得三棱锥B﹣PEC的体积.
解:(I)∵△ABC中,D、E分别为AB、AC中点,∴DE∥BC
∵DE面PBC且BC面PBC,∴DE∥面PBC;
(II)连结PD
∵PA=PB,D为AB中点,∴PD⊥AB
∵DE∥BC,BC⊥AB,∴DE⊥AB,
又∵PD、DE是平面PDE内的相交直线,∴AB⊥平面PDE
∵PE平面PDE,∴AB⊥PE;
(III)∵PD⊥AB,平面PAB⊥平面ABC,平面PAB∩平面ABC=AB
∴PD⊥平面ABC,可得PD是三棱锥P﹣BEC的高
又∵PD=![]() ,S△BEC=
,S△BEC=![]() S△ABC=
S△ABC=![]()
∴三棱锥B﹣PEC的体积V=VP﹣BEC=![]() S△BEC×PD=
S△BEC×PD=![]()


科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①“若![]() 为
为![]() 的极值点,则
的极值点,则![]() ”的逆命题为真命题;
”的逆命题为真命题;
②“平面向量![]() 的夹角是钝角”的充分不必要条件是
的夹角是钝角”的充分不必要条件是![]()
③若命题![]() ,则
,则![]()
④函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
其中不正确的个数是
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义在![]() 上的函数
上的函数![]() ,其图象是连续不断的,且存在常数
,其图象是连续不断的,且存在常数![]() 使得
使得![]() 对任意的实数
对任意的实数![]() 都成立,则称
都成立,则称![]() 是一个“
是一个“![]() 特征函数”则下列结论中正确的个数为( ).
特征函数”则下列结论中正确的个数为( ).
①![]() 是常数函数中唯一的“
是常数函数中唯一的“![]() 特征函数”;
特征函数”;
②![]() 不是“
不是“![]() 特征函数”;
特征函数”;
③“![]() 特征函数”至少有一个零点;
特征函数”至少有一个零点;
④![]() 是一个“
是一个“![]() 特征函数”;.
特征函数”;.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1的方程为3x+4y﹣12=0.
(1)若直线l2与l1平行,且过点(﹣1,3),求直线l2的方程;
(2)若直线l2与l1垂直,且l2与两坐标轴围成的三角形面积为4,求直线l2的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的容积为![]() 立方米,且l≥2r.假设该容器的建造费用仅与其表面积有关,已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为c(c>3)千元.设该容器的建造费用为y千元.
立方米,且l≥2r.假设该容器的建造费用仅与其表面积有关,已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为c(c>3)千元.设该容器的建造费用为y千元.
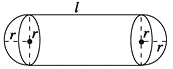
①写出y关于r的函数表达式,并求该函数的定义域;
②求该容器的建造费用最小时的r.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】桑基鱼塘是某地一种独具地方特色的农业生产形式,某研究单位打算开发一个桑基鱼塘项目,该项目准备购置一块![]() 平方米的矩形地块,中间挖成三个矩形池塘养鱼,挖出的泥土堆在池塘四周形成基围(阴影部分所示)种植桑树,池塘周围的基围宽均为
平方米的矩形地块,中间挖成三个矩形池塘养鱼,挖出的泥土堆在池塘四周形成基围(阴影部分所示)种植桑树,池塘周围的基围宽均为![]() 米,如图,设池塘所占总面积为
米,如图,设池塘所占总面积为![]() 平方米.
平方米.
(Ⅰ)试用![]() 表示
表示![]() .
.
(Ⅱ)当![]() 取何值时,才能使得
取何值时,才能使得![]() 最大?并求出
最大?并求出![]() 的最大值.
的最大值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】树立和践行“绿水青山就是金山银山,坚持人与自然和谐共生”的理念越来越深入人心,已形成了全民自觉参与,造福百姓的良性循环.据此,某网站推出了关于生态文明建设进展情况的调查,调查数据表明,环境治理和保护问题仍是百姓最为关心的热点,参与调查者中关注此问题的约占![]() .现从参与关注生态文明建设的人群中随机选出
.现从参与关注生态文明建设的人群中随机选出![]() 人,并将这
人,并将这![]() 人按年龄分组:第
人按年龄分组:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

(Ⅰ)求出![]() 的值;
的值;
(Ⅱ)求出这![]() 人年龄的样本平均数(同一组数据用该区间的中点值作代表)和中位数(精确到小数点后一位);
人年龄的样本平均数(同一组数据用该区间的中点值作代表)和中位数(精确到小数点后一位);
(Ⅲ)现在要从年龄较小的第![]() 、
、![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 人,则第
人,则第![]() 、
、![]() 组分别抽取多少人?
组分别抽取多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com