
矩形
ABCD,AB=3,BC=4,沿对角线BD把△ABD折起,使点A在平面BCD上的射影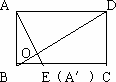
|
这是一道由平面图形折叠成立体图形的问题,解决问题的关键在于搞清折叠前后“变”与“不变”.结果在平面图形中过 A作AE⊥BD交BD于O、交BC于E,则折叠后OA、OE与BD的垂直关系不变.但OA与OE此时变成相交两线段并确定一平面,此平面必与棱垂直.由特征Ⅱ可知,面AOE与面ABD、面CBD的交线OA与OE所成的角,即为所求二面角的平面角.另外,A在面BCD上的射影必在OE所在的直线上,又题设射影落在BC上,所以E点就是
|


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:
水平放置的矩形ABCD长AB=4,宽BC=2,以AB、AD为轴作出斜二测直观图A′B′C′D′,则四边形A′B′C′D′的面积为( )
A.4![]()
B.2![]()
C.4
D.2
查看答案和解析>>
科目:高中数学 来源:2012年全国普通高等学校招生统一考试理科数学(浙江卷解析版) 题型:选择题
已知矩形ABCD,AB=1,BC=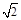 .将
.将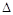 ABD沿矩形的对角线BD所在的直线进行翻着,在翻着过程中,
ABD沿矩形的对角线BD所在的直线进行翻着,在翻着过程中,
A.存在某个位置,使得直线AC与直线BD垂直
B.存在某个位置,使得直线AB与直线CD垂直
C.存在某个位置,使得直线AD与直线BC垂直
D.对任意位置,三直线“AC与BD”,“AB与CD”,“AD与BC”均不垂直
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省杭西高高三上学期11月月考文科数学试卷(解析版) 题型:填空题
如图,已知矩形ABCD,AB=2,AD=1.若点E,F,G,H分别在线段AB,BC,CD,DA上,且AE=BF=CG=DH,则四边形EFGH面积的最小值为 .
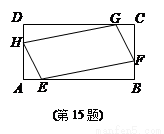
查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省高三高考样卷数学文卷 题型:填空题
如图,已知矩形ABCD,AB=2,AD=1.若点E,F,G,H分别在线段AB,BC,CD,DA上,且AE=BF=CG=DH,则四边形EFGH面积的最小值为________.
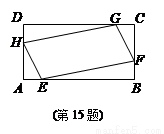
查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省高三高考样卷数学文卷 题型:填空题
如图,已知矩形ABCD,AB=2,AD=1.若点E,F,G,H分别在线段AB,BC,CD,DA上,且AE=BF=CG=DH,则四边形EFGH面积的最小值为________.
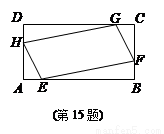
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com