
【题目】已知函数![]() .
.
(![]() )当
)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程.
处的切线方程.
(![]() )如果函数
)如果函数![]() 在
在![]() 上单调递减,求
上单调递减,求![]() 的取值范围.
的取值范围.
(![]() )当
)当![]() 时,讨论函数
时,讨论函数![]() 零点的个数.
零点的个数.
【答案】(![]() )
)![]() .(
.(![]() )
)![]() .(
.(![]() )见解析.
)见解析.
【解析】试题分析: ![]() 求出当
求出当![]() 时的
时的![]() 的解析式,求出导数,求得切线的斜率和切点,即可求得切线方程为
的解析式,求出导数,求得切线的斜率和切点,即可求得切线方程为![]() ;
;
![]() 由
由![]() 在
在![]() 上单调递减,等价于
上单调递减,等价于![]() 在
在![]() 上恒成立,变形得到
上恒成立,变形得到![]() 恒成立,运用基本不等式求得右边的最小值,即可得到
恒成立,运用基本不等式求得右边的最小值,即可得到![]() 的取值范围;
的取值范围;
![]() 求出
求出![]() ,求得单调区间和最小值,讨论最小值的符号,对
,求得单调区间和最小值,讨论最小值的符号,对![]() 讨论,当当
讨论,当当![]() 时,当
时,当![]() 时,当
时,当![]() 时,讨论函数的单调性,即可判断零点的个数
时,讨论函数的单调性,即可判断零点的个数
解析:(![]() )当
)当![]() 时,
时, ![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
,
∴![]() 在点
在点![]() 处的切线方程为:
处的切线方程为: ![]() ,即
,即![]() .
.
(![]() )函数
)函数![]() 在
在![]() 上单调递减,
上单调递减,
等价于![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 恒成立,
恒成立,
∵![]() ,当且仅当
,当且仅当![]() ,
,
即![]() 时,等号成立.
时,等号成立.
∴![]() ,即
,即![]() 的取值范围是
的取值范围是![]() .
.
(![]() )
)![]() ,
,
令![]() ,得
,得![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() 单调递减;
单调递减;
当![]() 时,
时, ![]() ,
, ![]() 单调递增,
单调递增,
∴![]() .
.
①当![]() 时,
时, ![]() ,
, ![]() 在定义域内无零点;
在定义域内无零点;
②当![]() 时,
时, ![]() ,则
,则![]() 在定义域内有唯一的零点;
在定义域内有唯一的零点;
③当![]() 时,
时, ![]() ,
,
由![]() ,
,
所以![]() 在增区间
在增区间![]() 内有唯一零点;
内有唯一零点;
![]() ,
,
设![]() ,则
,则![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,即
,即![]() ,
,
∴![]() 在减区间
在减区间![]() 内有唯一的零点,
内有唯一的零点,
则![]() 时,
时, ![]() 在定义域内有两个两点,
在定义域内有两个两点,
综上所述:当![]() 时,
时, ![]() 在定义域内无零点;
在定义域内无零点;
当![]() 时,
时, ![]() 在定义域内有唯一的两点;
在定义域内有唯一的两点;
当![]() 时,
时, ![]() 在定义域内有两个零点.
在定义域内有两个零点.


科目:高中数学 来源: 题型:
【题目】 已知△ABC的三个内角A,B,C的对边分别为a,b,c,向量m=![]() ,n=
,n=![]() ,且m与n的夹角为
,且m与n的夹角为![]() .
.
(1)求角C;
(2)已知c=![]() ,S△ABC=
,S△ABC=![]() ,求a+b的值.
,求a+b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在流行病学调查中,潜伏期指自病原体侵入机体至最早临床症状出现之间的一段时间.某地区一研究团队从该地区500名A病毒患者中,按照年龄是否超过60岁进行分层抽样,抽取50人的相关数据,得到如下表格:
潜伏期(单位:天) |
|
|
|
|
|
|
| |
人 数 | 60岁及以上 | 2 | 5 | 8 | 7 | 5 | 2 | 1 |
60岁以下 | 0 | 2 | 2 | 4 | 9 | 2 | 1 | |
(1)估计该地区500名患者中60岁以下的人数;
(2)以各组的区间中点值为代表,计算50名患者的平均潜伏期(精确到0.1);
(3)从样本潜伏超过10天的患者中随机抽取两人,求这两人中恰好一人潜伏期超过12天的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 满足
满足![]() (
(![]() ),且
),且![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)若函数![]() 在区间
在区间![]() 上是单调函数,求实数
上是单调函数,求实数![]() 的取值范围;
的取值范围;
(3)若关于![]() 的方程
的方程![]() 有区间
有区间![]() 上有一个零点,求实数
上有一个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
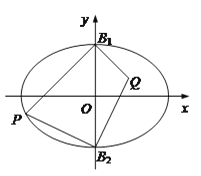
【题目】如图,在平面直角坐标系xOy中,B1,B2是椭圆![]() 的短轴端点,P是椭圆上异于点B1,B2的一动点.当直线PB1的方程为
的短轴端点,P是椭圆上异于点B1,B2的一动点.当直线PB1的方程为![]() 时,线段PB1的长为
时,线段PB1的长为![]() .
.
(1)求椭圆的标准方程;
(2)设点Q满足: ![]()
![]() .求证:△PB1B2与△QB1B2的面积之比为定值.
.求证:△PB1B2与△QB1B2的面积之比为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 定义在实数集
定义在实数集![]() 上的函数,把方程
上的函数,把方程![]() 称为函数
称为函数![]() 的特征方程,特征方程的两个实根
的特征方程,特征方程的两个实根![]() ,
,![]()
![]() 称为
称为![]() 的特征根.
的特征根.
(1)讨论函数的奇偶性,并说明理由;
(2)求![]() 表达式;
表达式;
(3)把函数![]() ,
,![]() 的最大值记作
的最大值记作![]() 、最小值记作
、最小值记作![]() ,令
,令![]() ,若
,若![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com