

科目:高中数学 来源:不详 题型:解答题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 阅读过莫言的 作品数(篇) | 0~25 | 26~50 | 51~75 | 76~100 | 101~130 |
| 男生 | 3 | 6 | 11 | 18 | 12 |
| 女生 | 4 | 8 | 13 | 15 | 10 |
| | 非常了解 | 一般了解 | 合计 |
| 男生 | | | |
| 女生 | | | |
| 合计 | | | |

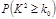 | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
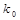 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
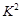 有两个临界值:3.841和6.635;当
有两个临界值:3.841和6.635;当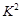 >3.841时,有95%的把握说明两个事件有关,当
>3.841时,有95%的把握说明两个事件有关,当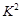 >6.635时,有99%的把握说明两个事件有关,当
>6.635时,有99%的把握说明两个事件有关,当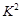
 3.841时,认为两个事件无关.在一项打鼾与患心脏病的调查中,共调查了2000人,经计算的
3.841时,认为两个事件无关.在一项打鼾与患心脏病的调查中,共调查了2000人,经计算的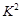 ="20." 87,根据这一数据分析,认为打鼾与患心脏病之间
="20." 87,根据这一数据分析,认为打鼾与患心脏病之间 | A.有95%的把握认为两者有关 |
| B.约有95%的打鼾者患心脏病 |
| C.有99%的把握认为两者有关 |
| D.约有99%的打鼾者患心脏病 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| | 支持A方案 | 支持B方案 | 支持C方案 |
| 35岁以下 | 200 | 400 | 800 |
| 35岁以上(含35岁) | 100 | 100 | 400 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| x | 0 | 1 | 2 | 3 |
| y | 0 | 2 | 6 | 7 |
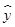 =
= x+
x+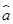 必过点( )
必过点( )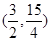 D.(3,7)
D.(3,7)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 智力评分 | 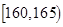 | 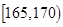 |  | 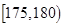 | 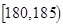 |  |
| 频数 | 2 | 5 | 14 | 13 | 4 | 2 |
| 智力评分 | 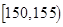 |  | 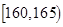 | 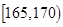 |  | 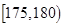 |
| 频数 | 1 | 7 | 12 | 6 | 3 | 1 |

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
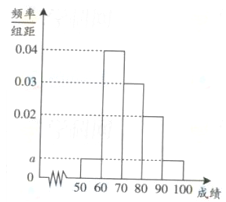
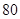 小时的社区服务才合格.教育部门在全市随机抽取200位学生参加社区服务的数据,按时间段
小时的社区服务才合格.教育部门在全市随机抽取200位学生参加社区服务的数据,按时间段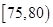 ,
, ,
,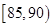 ,
,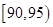 ,
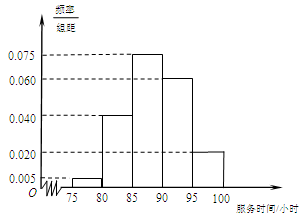
,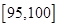 (单位:小时)进行统计,其频率分布直方图如图所示.
(单位:小时)进行统计,其频率分布直方图如图所示.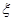 为3位学生中参加社区服务时间不少于90小时的人数.试求随机变量
为3位学生中参加社区服务时间不少于90小时的人数.试求随机变量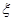 的分布列和数学期望
的分布列和数学期望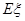 .
.
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
零件数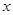 (个) (个) | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
加工时间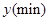 | 62 | 68 | 75 | 81 | 89 | 95 | 102 | 108 |
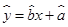 ,则点
,则点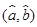 在直线
在直线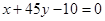 的( )
的( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com