
分析 (1)由题意列关于a,b,c的方程组,求解方程组可得a,b的值,则椭圆方程可求;
(2)由题意设出直线l的方程,与椭圆方程联立,化为关于y的一元二次方程,利用根与系数的关系求得|y1-y2|,代入三角形面积公式,换元后利用基本不等式求得最值.
解答 解.(1)由题意,$\left\{\begin{array}{l}{e=\frac{c}{a}=\frac{\sqrt{3}}{2}}\\{2b=2}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得a=2,b=1,
故椭圆的标准方程为$\frac{x^2}{4}+{y^2}=1$;
(2)存在△AOB面积的最大值.
∵直线l过点E(-1,0),可设直线l的方程为 x=my-1.
则$\left\{\begin{array}{l}\frac{x^2}{4}+{y^2}=1\\ x=my-1.\end{array}\right.$,整理得(m2+4)y2-2my-3=0.
由△=(2m)2+12(m2+4)>0.
设A(x1,y1),B(x2,y2).
则${y}_{1}+{y}_{2}=\frac{2m}{{m}^{2}+4},{y}_{1}{y}_{2}=\frac{-3}{{m}^{2}+4}$.
∴|y1-y2|=$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=$\frac{4\sqrt{{m}^{2}+3}}{{m}^{2}+4}$.
∴${S_{△AOB}}=\frac{1}{2}|{OE}|•|{{y_1}-{y_2}}|$=$\frac{{2\sqrt{{m^2}+3}}}{{{m^2}+4}}=\frac{2}{{\sqrt{{m^2}+3}+\frac{1}{{\sqrt{{m^2}+3}}}}}$.
设$g(t)=t+\frac{1}{t}$,$t=\sqrt{{m^2}+3}$,$t≥\sqrt{3}$.
则g(t)在区间$[\sqrt{3},+∞)$上为增函数,
∴$g(t)≥\frac{{4\sqrt{3}}}{3}$.
∴${S_{△AOB}}≤\frac{{\sqrt{3}}}{2}$,当且仅当m=0时取等号,即${({S_{△AOB}})_{max}}=\frac{{\sqrt{3}}}{2}$.
∴S△AOB的最大值为$\frac{{\sqrt{3}}}{2}$.
点评 本题考查椭圆的简单性质,考查了直线与椭圆位置关系的应用,体现了“设而不求”的解题思想方法,训练了利用基本不等式求最值,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,1) | B. | [-2,1) | C. | [-1,2) | D. | (-1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” | |
| B. | 命题“?x≥0,x2+x-1<0”的否定是“?x<0,x2+x-1<0” | |
| C. | “x=-1”是“x2-5x-6=0”的必要不充分条件 | |
| D. | 命题“若x=y,则sinx=siny”的逆否命题为真命题. |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
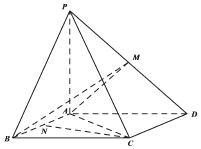 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥底面ABCD,M是棱PD的中点,且PA=AB=AC=2,BC=2$\sqrt{2}$.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥底面ABCD,M是棱PD的中点,且PA=AB=AC=2,BC=2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | -7 | C. | $\frac{1}{8}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com