练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    平面ABCD中，点A坐标为（0，1，1），点B坐标为（1，2，1），点C坐标为（-1，0，-1）．若向量
    a
    =（-2，y，z），且
    a
    为平面ABC的法向量，则yz=（　　）
    A．2B．0C．1D．-1
    AB
    =(1，1，0)    ，
    AC
    =(-1，-1，-2)    ，
    与平面ABC垂直的向量应与上面的向量的数量积为零，
    向量
    a
    =（-2，y，z），且
    a
    为平面ABC的法向量，
    则
    a
    ⊥
    AB
    且
    a
    ⊥
    AC
    ，即
    a
    •
    AB
    =0，且
    a
    •
    AC
    =0，即
    -2+y+0=0且2-y-2z=0，
    即
    y=2
    z=0
    ，
    ∴则yz=20=1，
    故选C．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    平面ABCD中，点A坐标为（0，1，1），点B坐标为（1，2，1），点C坐标为（-1，0，-1）．若向量
    a
    =（-2，y，z），且
    a
    为平面ABC的法向量，则yz=（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在复平面内的?ABCD中，点A，B，C分别对应复数4+i，3+4i，3-5i，则点D对应的复数是（　　）
    A、2-3iB、4+8iC、4-8iD、1+4i

    查看答案和解析>>

    科目：高中数学 来源：2012年全国普通高等学校招生统一考试理科数学（浙江卷解析版） 题型：解答题

    如图，在四棱锥P—ABCD中，底面是边长为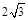的菱形，且∠BAD＝120°，且PA⊥平面ABCD，PA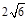＝，M，N分别为PB，PD的中点．

    (Ⅰ)证明：MN∥平面ABCD；

    (Ⅱ) 过点A作AQ⊥PC，垂足为点Q，求二面角A—MN—Q的平面角的余弦值．

     

    查看答案和解析>>

    科目：高中数学 来源：2008-2009学年广东省广州市越秀区育才中学高二（下）模块数学试卷（理科）（必修2+选修2-1）（解析版） 题型：选择题

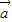    平面ABCD中，点A坐标为（0，1，1），点B坐标为（1，2，1），点C坐标为（-1，0，-1）．若向量=（-2，y，z），且为平面ABC的法向量，则yz=（ ）
    A．2
    B．0
    C．1
    D．-1

    查看答案和解析>>

    同步练习册答案