
分析 由题意可得an+1-an=2(an-an-1),数列{an-an-1}为首项为1,公比为2的等比数列,运用等比数列的通项公式和数列恒等式an=a1+(a2-a1)+(a3-a2)+…+(an-an-1),再由等比数列的求和公式,即可得到所求.
解答 解:an+1-3an+2an-1=0,即为an+1-an=2(an-an-1),
数列{an-an-1}为首项为1,公比为2的等比数列,
即有an-an-1=2n-2(n>1),
则an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)
=1+1+2+4+…+2n-2=1+$\frac{1-{2}^{n-1}}{1-2}$=2n-1,
则前n项的和Sn=$\frac{1-{2}^{n}}{1-2}$=2n-1.
点评 本题考查等比数列的通项和求和公式的运用,考查数列恒等式的运用及构造数列的思想,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 0 | C. | 1 | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年安徽豪州蒙城县一中高二上月考一数学试卷(解析版) 题型:解答题
设数列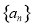 的前
的前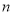 项和为
项和为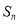 ,
,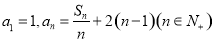 .
.
(1)证明:数列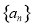 为等差数列,并分别求出
为等差数列,并分别求出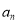 和
和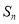 ;
;
(2)设数列 的前
的前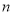 项和为
项和为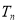 ,证明:
,证明: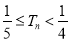 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 27 | B. | 16 | C. | 9 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 很大的实数可以构成集合 | |
| B. | 自然数集N中最小的数是1 | |
| C. | 集合{y|y=x2-1}与集合{(x,y)|y=x2-1}是同一个集合 | |
| D. | 空集是任何集合的子集. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com