
【题目】已知函数![]() 的部分图象如图所示,则下列判断正确的是( )
的部分图象如图所示,则下列判断正确的是( )
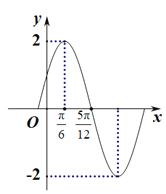
A. 函数的图象关于点![]() 对称
对称
B. 函数的图象关于直线![]() 对称
对称
C. 函数![]() 的最小正周期为
的最小正周期为![]()
D. 当![]() 时,函数
时,函数![]() 的图象与直线
的图象与直线![]() 围成的封闭图形面积为
围成的封闭图形面积为![]()
【答案】D
【解析】
由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,可得f(x)的解析式,再根据余弦函数的图象和性质,判断各个选项是否正确,从而得出结论.
解:函数![]() 的部分图象,可得A=2,
的部分图象,可得A=2,![]()
![]() ,∴ω=2.
,∴ω=2.
再根据五点法作图可得2![]() φ
φ![]() ,∴φ
,∴φ![]() ,f(x)=2sin(2x
,f(x)=2sin(2x![]() ).
).
令x![]() ,求得f(x)=﹣2,为函数的最小值,故A错误;
,求得f(x)=﹣2,为函数的最小值,故A错误;
令x![]() ,求得f(x)=﹣1,不是函数的最值,故B错误;
,求得f(x)=﹣1,不是函数的最值,故B错误;
函数f(2x)=2sin(4x![]() )的最小正周期为
)的最小正周期为![]() ,故C错误;
,故C错误;
当![]() 时,
时,![]() 2x
2x![]() ,函数f(x)的图象与直线y=2围成的封闭图形为x
,函数f(x)的图象与直线y=2围成的封闭图形为x![]() 、x
、x![]() 、y=2、y=﹣2构成的矩形的面积的一半,
、y=2、y=﹣2构成的矩形的面积的一半,
矩形的面积为π(2+2)=4π,故函数f(x)的图象与直线y=2围成的封闭图形面积为2π,
故D正确,
故选:D.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
【题目】2020年春节突如其来的新型冠状病毒肺炎在湖北爆发,为了打赢疫情防控阻击战,我们执行了延长假期政策,在延长假期面前,我们“停课不停学”,河南省教育厅组织部分优秀学校的优秀教师录播《名师同步课堂》,我校高一年级要在甲、乙、丙、丁、戊5位数学教师中随机抽取3人参加录播课堂,则甲、乙两位教师同时被选中的概率为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)有物理、化学、生物三个学科竞赛各设冠军一名,现有![]() 人参赛可报任意学科并且所报学科数不限,则最终决出冠军的结果共有多少种可能?
人参赛可报任意学科并且所报学科数不限,则最终决出冠军的结果共有多少种可能?
(2)有![]() 共
共![]() 个数,从中取
个数,从中取![]() 个数排成一个五位数,要求奇数位上只能是奇数,则共可排成多少个五位数?
个数排成一个五位数,要求奇数位上只能是奇数,则共可排成多少个五位数?
(3)有![]() 共
共![]() 个数,从中取
个数,从中取![]() 个数排成一个五位数,要求奇数只在奇数位上,则共可排成多少个五位数?
个数排成一个五位数,要求奇数只在奇数位上,则共可排成多少个五位数?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点 .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过椭圆![]() 左焦点的直线
左焦点的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,直线
两点,直线![]() 过坐标原点且直线
过坐标原点且直线![]() 与
与![]() 的斜率互为相反数,直线
的斜率互为相反数,直线![]() 与椭圆交于
与椭圆交于![]() 两点且均不与点
两点且均不与点![]() 重合,设直线
重合,设直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() .证明:
.证明: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方体ABCD-A1B1C1D1的棱长为4,E为棱CC1的中点,点M在正方形BCC1B1内运动,且直线AM∥平面A1DE,则动点M的轨迹长度为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究黏虫孵化的平均温度![]() (单位:
(单位: ![]() )与孵化天数
)与孵化天数![]() 之间的关系,某课外兴趣小组通过试验得到如下6组数据:
之间的关系,某课外兴趣小组通过试验得到如下6组数据:
组号 | 1 | 2 | 3 | 4 | 5 | 6 |
平均温度 | 15.3 | 16.8 | 17.4 | 18 | 19.5 | 21 |
孵化天数 | 16.7 | 14.8 | 13.9 | 13.5 | 8.4 | 6.2 |
他们分别用两种模型①![]() ,②
,②![]() 分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图:
分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图:

经计算得![]() ,
,
(1)根据残差图,比较模型①,②的拟合效果,应选择哪个模型?(给出判断即可,不必说明理由)
(2)残差绝对值大于1的数据被认为是异常数据,需要剔除,剔除后应用最小二乘法建立![]() 关于
关于![]() 的线性回归方程.(精确到0.1)
的线性回归方程.(精确到0.1)
 ,.
,.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com