
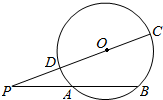
 自圆O外一点P引圆O的两条割线PAB和PDC,如图所示,其中割线PDC过圆心O.AB=$\sqrt{2}$OA,PD=$\sqrt{3}$,∠P=15°,
自圆O外一点P引圆O的两条割线PAB和PDC,如图所示,其中割线PDC过圆心O.AB=$\sqrt{2}$OA,PD=$\sqrt{3}$,∠P=15°,分析 (1)证明∠AOB=90°,可得∠POA+(180°-2∠C)=90°,即可求∠PCB的大小;
(2)利用正弦定理,可得PA=$\frac{\sqrt{3}+R}{\sqrt{2}}$.根据割线定理有PA•PB=PD•PC,求出R,即可求出线段BC和PA的长度.
解答 解:(1)∵AB=$\sqrt{2}$OA,OA=OB,
∴∠AOB=90°,
∴∠POA+(180°-2∠C)=90°,
∵∠P=15°,
∴∠POA=∠OAB-∠P=30°,
∴30°+(180°-2∠C)=90°,
∴∠C=60°;
(2)设圆O的半径为R,在△PAO中,$\frac{PA}{sin30°}=\frac{\sqrt{3}}{sin135°}$,
∴PA=$\frac{\sqrt{3}+R}{\sqrt{2}}$.
根据割线定理有PA•PB=PD•PC,
∴$\frac{\sqrt{3}+R}{\sqrt{2}}$•($\frac{\sqrt{3}+R}{\sqrt{2}}$+$\sqrt{2}$R)=$\sqrt{3}$($\sqrt{3}$+2R),
∴R=1,
∴PA=$\frac{\sqrt{6}+\sqrt{2}}{2}$,
∵∠BOC=60°,
∴△BOC为等边三角形,
∴BC=1.
点评 本题考查角的计算,考查割线定理,考查学生的计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{ln2}{2},\frac{1}{e})$ | B. | $(0,\frac{1}{2})$ | C. | $(0,\frac{1}{e})$ | D. | $(\frac{1}{e},\frac{1}{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
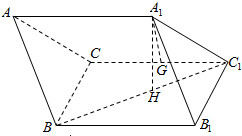 在三棱柱ABC-A1B1C1中,面BB1C1C是边长为2的正方形,点A1在平面BB1C1C上的射影H是BC1的中点,且A1H=$\sqrt{3}$,G是CC1的中点.
在三棱柱ABC-A1B1C1中,面BB1C1C是边长为2的正方形,点A1在平面BB1C1C上的射影H是BC1的中点,且A1H=$\sqrt{3}$,G是CC1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com