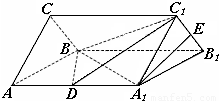
分析:(1)在线段BC1上取中点F,连接EF、DF,通过证出四边形EFDA1是平行四边形,得出A1E∥FD后,即可证明A1E∥平面BDC1
(2)由正棱锥的性质,可以证明A1E⊥面CC1B1B,而由(1)A1E∥FD,所以FD⊥面CC1B1B,BF是BD在平面CC1B1B上的射影,∠DBF是BD与平面CC1B1B所成 的角.在RT△DFB中求解即可.
解答: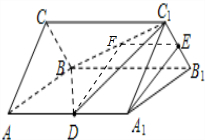
(1)证明:在线段BC
1上取中点F,连接EF、DF,
∵E是 B
1C
1的中点,∴EF是△C
1B
1B的中位线.
则由题意得EF∥DA
1,且EF=DA
1,
∴四边形EFDA
1是平行四边形
∴A
1E∥FD,又A
1E?平面BDC
1,FD?平面BDC
1∴A
1E∥平面BDC
1(2)解:E是正△A
1B
1C
1的边B
1C
1的中点,
∴A
1E⊥B
1C
1
由正棱锥的性质,面A
1B
1C
1⊥面CC
1B
1B,且面A
1B
1C
1∩面CC
1B
1B=B1C1,
∴A
1E⊥面CC
1B
1B,
由(1)A
1E∥FD,
∴FD⊥面CC
1B
1B,
∴BF是BD在平面CC
1B
1B上的射影,∠DBF是BD与平面CC
1B
1B所成 的角.
∵DF=A
1E=
=
=
2.
在RT△DAB中,DB=
=
=4
.
∴在RT△DFB中,sin∠DBF=
=
=.
点评:本题考查直线和平面垂直关系的判定,线面角求解.考查空间想象、转化、计算等能力.

 如图:D、E分别是正三棱柱ABC-A1B1C1的棱AA1、B1C1的中点,且棱AA1=8,AB=4,
如图:D、E分别是正三棱柱ABC-A1B1C1的棱AA1、B1C1的中点,且棱AA1=8,AB=4, (1)证明:在线段BC1上取中点F,连接EF、DF,
(1)证明:在线段BC1上取中点F,连接EF、DF,

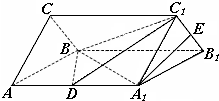 如图,D、E分别是正三棱柱ABC-A1B1C1的棱AA1、BB1的中点,且棱AA1=8,AB=4.
如图,D、E分别是正三棱柱ABC-A1B1C1的棱AA1、BB1的中点,且棱AA1=8,AB=4.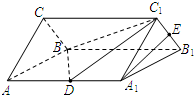 (2009•孝感模拟)如图:D、E分别是正三棱柱ABC-A1B1C1的棱AA1、B1C1的中点,且棱AA1=8,AB=4,
(2009•孝感模拟)如图:D、E分别是正三棱柱ABC-A1B1C1的棱AA1、B1C1的中点,且棱AA1=8,AB=4,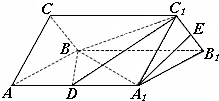 如图,D、E分别是正三棱柱ABC-A1B1C1的棱AA1、BB1的中点,且棱AA1=8,AB=4.
如图,D、E分别是正三棱柱ABC-A1B1C1的棱AA1、BB1的中点,且棱AA1=8,AB=4.