
分析 (1)利用极值的意义,建立方程,即可求a,b;
(2)设切点坐标.利用导数的几何意义求切线方程,然后利用切线过原点,确定切点坐标即可
解答 解:(1)f′(x)=3ax2+2bx-3,
依题意,f′(1)=f′(-1)=0,
即$\left\{\begin{array}{l}{3a+2b-3=0}\\{3a-2b-3=0}\end{array}\right.$,
解得a=1,b=0.
(2)曲线方程为y=x3-3x,点A(0,16)不在曲线上.
设切点为M(x0,y0),则点M的坐标满足y0=${{x}_{0}}^{3}$-3x0.
因f′(x0)=3(${{x}_{0}}^{2}$-1),故切线的方程为y-y0=3(${{x}_{0}}^{2}$-1)(x-x0)
注意到点A(0,16)在切线上,有16-(${{x}_{0}}^{3}$-3x0)=3( ${{x}_{0}}^{2}$-1)(0-x0),
化简得:${{x}_{0}}^{3}$=-8,解得x0=-2.
所以,切点为M(-2,-2),切线方程为9x-y+16=0.
点评 本题主要考查函数的单调性与极值,考查导数的几何意义,要注意过点的切线和在点处的切线的不同.


科目:高中数学 来源: 题型:选择题

| A. | AD•AB=CD2 | B. | CE•CB=AD•AB | C. | CE•CB=AD•DB | D. | CE•EB=CD2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1-2i | B. | 1+2i | C. | 2-i | D. | -2-i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
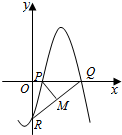 如图,函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|≤$\frac{π}{2}$)与坐标轴的三个交点P、Q、R满足P(1,0),M(2,-2)为线段QR的中点,则A=( )
如图,函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|≤$\frac{π}{2}$)与坐标轴的三个交点P、Q、R满足P(1,0),M(2,-2)为线段QR的中点,则A=( )| A. | 2$\sqrt{3}$ | B. | $\frac{7\sqrt{3}}{3}$ | C. | $\frac{8\sqrt{3}}{3}$ | D. | 4$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com