解:(1)函数g(x)=-x
3的定义域为 R,g′(x)=-3x
2≤0 (仅在x=0时取等号),
故函数g(x)在R上是减函数,故满足条件①.
若g(x)∈M,当x∈[a,b]时,
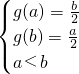
,即
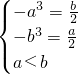
,解得
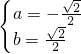
,故满足条件②的闭区间为[-

,

].
由此可得,g(x)属于集合M.
(2)函数h(x)的定义域是[1,+∞),当x>1时,
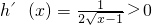
,故函数h(x)在[1,+∞)上是增函数,…
若h(x)∈M,则存在a,b∈[1,+∞),且a<b,使得
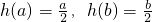
,即
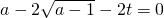
,且
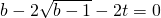
,…
令
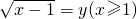
,则y≥0,
于是关于y的方程y
2-2y+1-2t=0在[0,+∞)上有两个不等的实根,…
记u(y)=y
2-2y+1-2t,∴
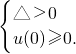
,∴
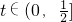
.…
分析:(1)函数g(x)的定义域为 R,利用导数求得函数g(x)在R上是减函数,故满足条件①.若g(x)∈M,当x∈[a,b]时,
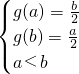
,解得a、b的值,可得满足条件②的闭区间存在,从而g(x)属于集合M.
(2)利用导数可得函数h(x)在定义域[1,+∞)上是增函数.若h(x)∈M,则存在a,b∈[1,+∞),且a<b,使得
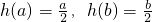
,即
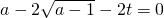
,且
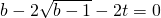
.令
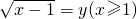
,则y≥0,于是关于y的方程y
2-2y+1-2t=0在[0,+∞)上有2个不等实根,利用二次函数的性质求得t的范围.
点评:本题主要考查函数的定义域、单调性的应用,求函数的最值,体现了转化的数学思想,属于中档题.

 ,最大值是
,最大值是 .请解答以下问题:
.请解答以下问题: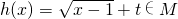 ,求实数t的取值范围.
,求实数t的取值范围.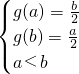 ,即
,即 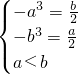 ,解得
,解得 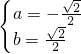 ,故满足条件②的闭区间为[-
,故满足条件②的闭区间为[- ,
, ].
].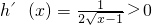 ,故函数h(x)在[1,+∞)上是增函数,…
,故函数h(x)在[1,+∞)上是增函数,…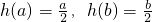 ,即
,即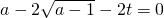 ,且
,且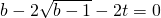 ,…
,…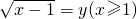 ,则y≥0,
,则y≥0,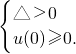 ,∴
,∴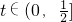 .…
.…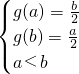 ,解得a、b的值,可得满足条件②的闭区间存在,从而g(x)属于集合M.
,解得a、b的值,可得满足条件②的闭区间存在,从而g(x)属于集合M.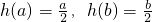 ,即
,即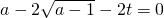 ,且
,且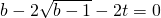 .令
.令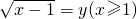 ,则y≥0,于是关于y的方程y2-2y+1-2t=0在[0,+∞)上有2个不等实根,利用二次函数的性质求得t的范围.
,则y≥0,于是关于y的方程y2-2y+1-2t=0在[0,+∞)上有2个不等实根,利用二次函数的性质求得t的范围.
