练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    设{an}是等差数列，{bn}为等比数列，其公比q≠1，且bi＞0（i=1、2、3 …n）若a1=b1，a11=b11则a6与b6的大小关系为    ．
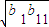
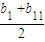
    【答案】分析：先根据等差中项的性质可知a1+a11=b1+b11=2a6，进而根据基本不等式≤，进而根据a1+a11=b1+b11，案可得．
    解答：解：∵a1=b1，a11=b11
    ∴a1+a11=b1+b11=2a6，
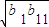
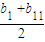
    ∵b6=≤=a6，当等号成立时有b1=b11，此时须有q=1，与已知矛盾，故等号不可能成立
    ∴b6＜a6，
    故答案为b6＜a6
    点评：本题主要考查了等差数列的性质．有些同学做错，是因为不能灵活运用等差中项和等比中项的定义及基本不等式．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    设{an}是等差数列，bn=（
    1
    2
    ）an．已知b1+b2+b3=
    21
    8
    ，b1b2b3=
    1
    8
    ．求等差数列的通项an．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设{an}是等差数列，a1+a3+a5=9，a6=9．则这个数列的前6项和等于（　　）
    A、12B、24C、36D、48

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    1、设{an}是等差数列，且a1+a5=6，则a3等于（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2011•惠州模拟）设{an}是等差数列，且a2+a3+a4=15，则这个数列的前5项和S5=（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设{an}是等差数列，a1＞0，a2007+a2008＞0，a2007•a2008＜0，则使Sn＞0成立的最大自然数n是（　　）

    查看答案和解析>>

    同步练习册答案