
 )是曲线f(x)=Asin(ωx+φ)(A>0,ω>0|φ|<
)是曲线f(x)=Asin(ωx+φ)(A>0,ω>0|φ|< )的一个最高点,且f(9-x)=f(9+x),曲线区间(1,9)内与x轴有唯一一个交点,求这个函数的解析式,并作出一个周期的图象.
)的一个最高点,且f(9-x)=f(9+x),曲线区间(1,9)内与x轴有唯一一个交点,求这个函数的解析式,并作出一个周期的图象. 解:∵点P(1,
解:∵点P(1, )是曲线f(x)=Asin(ωx+φ)(A>0,ω>0|φ|<
)是曲线f(x)=Asin(ωx+φ)(A>0,ω>0|φ|< )的一个最高点,
)的一个最高点, ,
,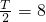
 ,ω=
,ω= ,
,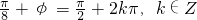 ,
,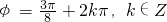 ,∵|φ|<
,∵|φ|< ,
,
 sin(
sin( x+
x+ ),
),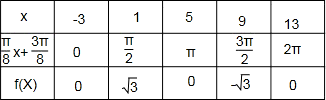 其图象如图所示:
其图象如图所示: )是曲线f(x)=Asin(ωx+φ)(A>0,ω>0|φ|<
)是曲线f(x)=Asin(ωx+φ)(A>0,ω>0|φ|< )的一个最高点,可知A=
)的一个最高点,可知A= ,由f(9-x)=f(9+x)得函数的一条对称轴方程为x=9,根据曲线区间(1,9)内与x轴有唯一一个交点,可知函数的周期,因此可求得函数的解析式;利用五点法列表,描点,即可画出函数的图象.
,由f(9-x)=f(9+x)得函数的一条对称轴方程为x=9,根据曲线区间(1,9)内与x轴有唯一一个交点,可知函数的周期,因此可求得函数的解析式;利用五点法列表,描点,即可画出函数的图象.

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:高中数学 来源: 题型:
| 1 |
| 64 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,直线l1和l2相交于点M且l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,|AM|=
如图,直线l1和l2相交于点M且l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,|AM|=| 17 |
查看答案和解析>>
科目:高中数学 来源: 题型:
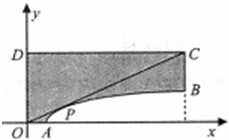 已知图形OAPBCD是由不等式组
已知图形OAPBCD是由不等式组
|
查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建师大附中高二(上)期末数学试卷(文科)(解析版) 题型:解答题
 如图,直线l1和l2相交于点M且l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,
如图,直线l1和l2相交于点M且l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形, ,|AN|=3,且|BN|=6.
,|AN|=3,且|BN|=6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com