
【题目】下列哪组中的函数f(x)与g(x)相等( )
A.f(x)=x2 , ![]()
B.f(x)=x+1,g(x)= ![]() +1
+1
C.f(x)=x,g(x)= ![]()
D.f(x)= ![]() ,g(x)=
,g(x)= ![]()
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga ![]() ,(a>0且a≠1).
,(a>0且a≠1).
(1)判断f(x)的奇偶性,并加以证明;
(2)是否存在实数m使得f(x+2)+f(m﹣x)为常数?若存在,求出m的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y= ![]() 的定义域是( )
的定义域是( )
A.[﹣ ![]() ,﹣1)∪(1,
,﹣1)∪(1, ![]() ]
]
B.(﹣ ![]() ,﹣1)∪(1,
,﹣1)∪(1, ![]() )??
)??
C.[﹣2,﹣1)∪(1,2]
D.(﹣2,﹣1)∪(1,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记函数 ![]() 的定义域为A,g(x)=lg[(x﹣a﹣1)(2a﹣x)](a<1)的定义域为B,求
的定义域为A,g(x)=lg[(x﹣a﹣1)(2a﹣x)](a<1)的定义域为B,求
(1)A,B;
(2)若BA,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() =(sin2x,2cos2x﹣1),
=(sin2x,2cos2x﹣1), ![]() =(sinθ,cosθ)(0<θ<π),函数f(x)=
=(sinθ,cosθ)(0<θ<π),函数f(x)= ![]()
![]() 的图象经过点(
的图象经过点( ![]() ,1).
,1).
(1)求θ及f(x)的最小正周期;
(2)当x∈ ![]() 时,求f(x)的最大值和最小值.
时,求f(x)的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在D上的函数f(x)若同时满足:①存在M>0,使得对任意的x1 , x2∈D,都有|f(x1)﹣f(x2)|<M;②f(x)的图象存在对称中心.则称f(x)为“P﹣函数”.
已知函数f1(x)= ![]() 和f2(x)=lg(
和f2(x)=lg( ![]() ﹣x),则以下结论一定正确的是( )
﹣x),则以下结论一定正确的是( )
A.f1(x)和 f2(x)都是P﹣函数
B.f1(x)是P﹣函数,f2(x)不是P﹣函数
C.f1(x)不是P﹣函数,f2(x)是P﹣函数
D.f1(x)和 f2(x)都不是P﹣函数
查看答案和解析>>
科目:高中数学 来源: 题型:
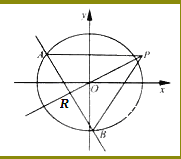
【题目】如图,椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,其左焦点到点
,其左焦点到点![]() 的距离为
的距离为![]() .不过原点O的直线
.不过原点O的直线![]() 与C相交于A,B两点,且线段AB被直线OP平分.
与C相交于A,B两点,且线段AB被直线OP平分.
(1)求椭圆C的方程;
(2)求![]() ABP的面积取最大时直线l的方程.
ABP的面积取最大时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某投资公司现提供两种一年期投资理财方案,一年后投资盈亏的情况如下表:
投资股市 | 获利 | 不赔不赚 | 亏损 | 购买基金 | 获利 | 不赔不赚 | 亏损 | |
概率 |
|
|
| 概率 |
|
|
|
(Ⅰ)甲、乙两人在投资顾问的建议下分别选择“投资股市”和“买基金”,若一年后他们中至少有一人盈利的概率大于![]() ,求
,求![]() 的取值范围;
的取值范围;
(Ⅱ)若![]() ,某人现有
,某人现有![]() 万元资金,决定在“投资股市”和“购买基金”这两种方案中选择出一种,那么选择何种方案可使得一年后的投资收益的数学期望值较大.
万元资金,决定在“投资股市”和“购买基金”这两种方案中选择出一种,那么选择何种方案可使得一年后的投资收益的数学期望值较大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com