
对于使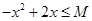 成立的所有常数
成立的所有常数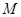 中,我们把
中,我们把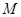 的最小值
的最小值 叫做
叫做 的上确界,若
的上确界,若 ,则
,则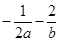 的上确界为 ( )
的上确界为 ( )
| A.-3 | B. | C.- | D. |
科目:高中数学 来源: 题型:单选题
当a,b,c∈(0,+∞)时,由 ≥
≥ ,
, ≥
≥ ,运用归纳推理,可猜测出的合理结论是( )
,运用归纳推理,可猜测出的合理结论是( )
A. ≥ ≥ (ai>0,i=1,2,…n) (ai>0,i=1,2,…n) |
B. ≥ ≥ (ai>0,i=1,2,…n) (ai>0,i=1,2,…n) |
C. ≥ ≥ (ai∈R,i=1,2,…n) (ai∈R,i=1,2,…n) |
D. ≥ ≥ (ai>0,i=1,2,…n) (ai>0,i=1,2,…n) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
若a>0,b>0,a+b=2,则下列不等式对一切满足条件的a,b恒成立的是________.(写出所有正确命题的编号)
①b≤1;② +
+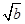 ≤
≤ ;③a2+b2≥2;④a3+b3≥3;⑤
;③a2+b2≥2;④a3+b3≥3;⑤ +
+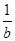 ≥2.
≥2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com