
设曲线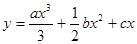 在点
在点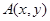 处的切线斜率为
处的切线斜率为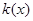 ,且
,且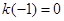 .对一切实数
.对一切实数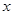 ,不等式
,不等式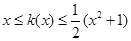 恒成立(
恒成立(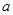 ≠0).
≠0).
(1) 求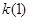 的值;
的值;
(2) 求函数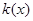 的表达式;
的表达式;
(3) 求证: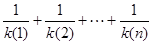 >
>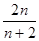 .
.
(1) 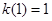 (2)
(2)  (3)
(3) 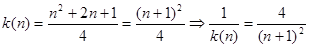 要证原不等式,即证
要证原不等式,即证 因为
因为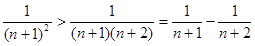
所以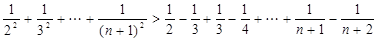
 =
=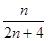 所以
所以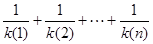
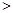

【解析】
试题分析:(1)由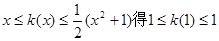 ,所以
,所以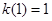 2分
2分
(2) ,由
,由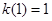 ,
,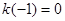 得 3分
得 3分
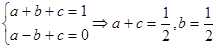 4分
4分
又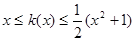 恒成立,则由
恒成立,则由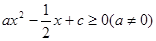 恒成立得
恒成立得

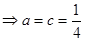 ,
6分
,
6分
同理由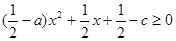 恒成立也可得:
恒成立也可得:  7分
7分
综上 ,
,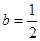 ,所以
,所以 8分
8分
(3)
要证原不等式,即证
因为
所以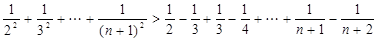
 =
=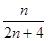
所以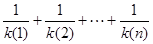
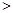
 12分
12分
本小问也可用数学归纳法求证。证明如下:
由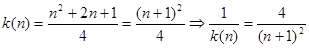
当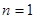 时,左边=1,右边=
时,左边=1,右边=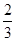 ,左边>右边,所以
,左边>右边,所以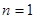 ,不等式成立
,不等式成立
假设当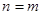 时,不等式成立,即
时,不等式成立,即
当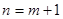 时,
时,
左边=

由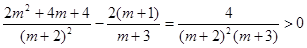
所以
即当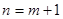 时,不等式也成立。综上得
时,不等式也成立。综上得 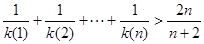
考点:函数导数,求函数解析式及不等式证明
点评:函数求解析式采用的是待定系数法,由已知条件找到 的关系式,期间将不等式恒成立问题转化为二次函数性质的考察,第三问在证明不等式时用到了放缩法,这种方法对学生有一定的难度
的关系式,期间将不等式恒成立问题转化为二次函数性质的考察,第三问在证明不等式时用到了放缩法,这种方法对学生有一定的难度


 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源:深圳实验学校高中部2006-2007学年度第一学期摸底考试 高三数学(理科) 题型:044
| |||||||||||||||
查看答案和解析>>
科目:高中数学 来源:2014届浙江瑞安瑞祥高级中学高二下学期期中考试理数学试卷(解析版) 题型:解答题
设曲线 在点
在点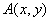 处的切线斜率为
处的切线斜率为 ,且
,且 ,对一切实数
,对一切实数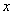 ,不等式
,不等式 恒成立
恒成立 .
.
(1)
求 的值;
的值;
(2)
求函数 的表达式;
的表达式;
(3)
求证: .
.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年山东省潍坊市高三开学摸底考试理科数学卷 题型:解答题
(本小题满分14分)
已知曲线 在点
在点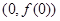 处的切线斜率为
处的切线斜率为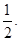
(1)求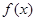 的极值;
的极值;
(2)设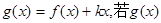 在(-∞,1)上是增函数,求实数
在(-∞,1)上是增函数,求实数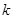 的取值范围;
的取值范围;
(3)若数列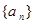 满足
满足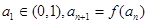 ,求证:对一切
,求证:对一切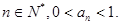
查看答案和解析>>
科目:高中数学 来源:2010-2011学年山东省潍坊市高三开学摸底考试理科数学卷 题型:解答题
(本小题满分14分)
已知曲线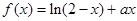 在点
在点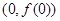 处的切线斜率为
处的切线斜率为
(1)求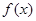 的极值;
的极值;
(2)设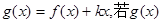 在(-∞,1)上是增函数,求实数
在(-∞,1)上是增函数,求实数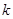 的取值范围;
的取值范围;
(3)若数列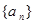 满足
满足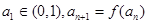 ,求证:对一切
,求证:对一切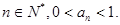
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com