
分析 利用等差中项和等比中项的性质求得sinα,sinβ与sinθ与cosθ的关系,进而利用同角三角函数的基本关系构造出等式,利用二倍角公式整理,即可得解.
解答 解:依题意可知2sinα=sinθ+cosθ,
sin2β=sinθcosθ,
∵cos2α-$\frac{1}{2}$cos2β=1-2sin2α-$\frac{1}{2}$(1-2sin2β)
=1-2($\frac{(sinθ+cosθ)^{2}}{4}$)-$\frac{1}{2}$(1-sin2θ)
=1-$\frac{1}{2}$-$\frac{1}{2}$sin2θ-$\frac{1}{2}$+$\frac{1}{2}$sin2θ=0.
故答案为:0.
点评 本题主要考查了三角函数的恒等变换及化简求值,考查了同角三角函数基本关系的运用,等差中项和等比中项的性质,属于中档题.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
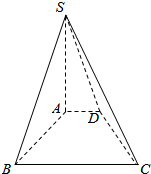 已知四棱锥S-ABCD中,底面ABCD是直角梯形,∠ABC=90°,AD∥BC,SA=AB=BC=2,AD=1,SA⊥底面ABCD.
已知四棱锥S-ABCD中,底面ABCD是直角梯形,∠ABC=90°,AD∥BC,SA=AB=BC=2,AD=1,SA⊥底面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | -$\frac{1}{3}$ | C. | 3 | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com