
【题目】集合L={l|l与直线y=x相交,且以交点的横坐标为斜率}.若直线l′∈L,点P(﹣1,2)到直线l′的最短距离为r,则以点P为圆心,r为半径的圆的标准方程为 .
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2﹣ax+a+3,g(x)=ax﹣2a.
(1)若函数h(x)=f(x)﹣g(x)在[﹣2,0]上有两个零点,求实数a的取值范围;
(2)若存在x0∈R,使得f(x0)≤0与g(x0)≤0同时成立,求实数a的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校举行“庆元旦”教工羽毛球单循环比赛(任意两个参赛队只比赛一场),共有高一、高二、高三三个队参赛,高一胜高二的概率为 ![]() ,高一胜高三的概率为
,高一胜高三的概率为 ![]() ,高二胜高三的概率为P,每场胜负独立,胜者记1分,负者记0分,规定:积分相同者高年级获胜.
,高二胜高三的概率为P,每场胜负独立,胜者记1分,负者记0分,规定:积分相同者高年级获胜.
(Ⅰ)若高三获得冠军概率为 ![]() ,求P.
,求P.
(Ⅱ)记高三的得分为X,求X的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若Sn为等差数列{an}的前n项和,且a1=1,S10=55.记bn=[lnan],其中[x]表示不超过x的最大整数,如[0.9]=0,[lg99]=1.则数列{bn}的前2017项和为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx+ax2(a∈R),y=f(x)的图象连续不间断.
(1)求函数y=f(x)的单调区间;
(2)当a=1时,设l是曲线y=f(x)的一条切线,切点是A,且l在点A处穿过函数y=f(x)的图象(即动点在点A附近沿曲线y=f(x)运动,经过点A时,从l的一侧进入另一侧),求切线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0).
=1(a>b>0).
(1)若椭圆的离心率为 ![]() ,且点(1,
,且点(1, ![]() )在椭圆上,
)在椭圆上,
①求椭圆的方程;
②设P(﹣1,﹣ ![]() ),R、S分别为椭圆C的右顶点和上顶点,直线PR和PS与y轴和x轴相交于点M,N,求直线MN的方程.
),R、S分别为椭圆C的右顶点和上顶点,直线PR和PS与y轴和x轴相交于点M,N,求直线MN的方程.
(2)设D(b,0),过D点的直线l与椭圆C交于E、F两点,且E、F均在y轴的右侧, ![]() =2
=2 ![]() ,求椭圆离心率的取值范围.
,求椭圆离心率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图扇形AOB是一个观光区的平面示意图,其中∠AOB的圆心角为 ![]() ,半径OA为1Km,为了便于游客观光休闲,拟在观光区内铺设一条从入口A到出口B的观光道路,道路由圆弧AC、线段CD及线段BD组成.其中D在线段OB上,且CD∥AO,设∠AOC=θ,
,半径OA为1Km,为了便于游客观光休闲,拟在观光区内铺设一条从入口A到出口B的观光道路,道路由圆弧AC、线段CD及线段BD组成.其中D在线段OB上,且CD∥AO,设∠AOC=θ,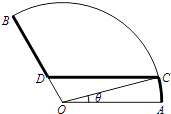
(1)用θ表示CD的长度,并写出θ的取值范围.
(2)当θ为何值时,观光道路最长?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图中,小方格是边长为1的正方形,图中粗线画出的是某几何体的三视图,且该几何体的顶点都在同一球面上,则该几何体的外接球的表面积为( )
A.32π
B.48π
C.50π
D.64π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1+2a2+…+nan=(n﹣1)2n+1+2,n∈N*
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn= ![]() ,Tn=b1+b2+…+bn , 求证:对任意的n∈N* , Tn<
,Tn=b1+b2+…+bn , 求证:对任意的n∈N* , Tn< ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com