
 已知函数$f(x)=2cosxsin({x+\frac{π}{3}})-\sqrt{3}{sin^2}x+sinxcosx$.
已知函数$f(x)=2cosxsin({x+\frac{π}{3}})-\sqrt{3}{sin^2}x+sinxcosx$.分析 (1)利用三角恒等变换,化简函数的解析式,可得该函数的最小正周期.
(2)用五点法作函数f(x)在$[{-\frac{π}{2},\frac{π}{2}}]$上的图象.
(3)由题意利用反正弦函数的定义,由f(x)=1,求得x的值,可得f-1(1)的值.
解答 解:(1)函数$f(x)=2cosxsin({x+\frac{π}{3}})-\sqrt{3}{sin^2}x+sinxcosx$=2cosx(sinx•$\frac{1}{2}$+cosx•$\frac{\sqrt{3}}{2}$)-$\sqrt{3}$•$\frac{1-cos2x}{2}$+$\frac{1}{2}$sin2x
=$\frac{1}{2}$sin2x+$\sqrt{3}$•$\frac{1+cos2x}{2}$-$\sqrt{3}$+$\frac{\sqrt{3}}{2}$cos2x+$\frac{1}{2}$sin2x=sin2x+$\sqrt{3}$cos2x=2sin(2x+$\frac{π}{3}$),
故该函数的最小正周期为$\frac{2π}{2}$=π.
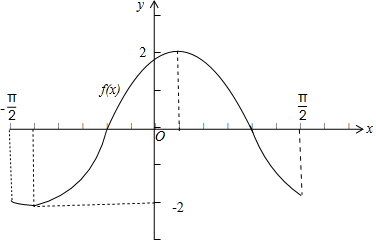
(2)画出函数f(x)在$[{-\frac{π}{2},\frac{π}{2}}]$上的图象,如图所示:
| 2x+$\frac{π}{3}$ | -$\frac{2π}{3}$ | -$\frac{π}{2}$ | 0 | $\frac{π}{2}$ | π | $\frac{4π}{3}$ |
| x | -$\frac{π}{2}$ | -$\frac{5π}{12}$ | -$\frac{π}{6}$ | $\frac{π}{12}$ | $\frac{π}{3}$ | $\frac{π}{2}$ |
| f(x) | -$\sqrt{3}$ | -2 | 0 | 2 | 0 | -$\sqrt{3}$ |
点评 本题主要考查三角恒等变换,用五点法作正弦函数的图象,反正弦函数的定义,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
| 每件产品A | 每件产品B | ||
| 研制成本、搭载 费用之和(万元) | 20 | 30 | 计划最大资金额 300万元 |
| 产品重量(千克) | 10 | 5 | 最大搭载重量110千克 |
| 预计收益(万元) | 80 | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量的标准,为了确定一个较为合理的标准,必须先了解全市居民日常用水量的分布情况.现采用抽样调查的方式,获得了n位居民某年的月均用水量(单位:),样本统计结果如图表:
我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量的标准,为了确定一个较为合理的标准,必须先了解全市居民日常用水量的分布情况.现采用抽样调查的方式,获得了n位居民某年的月均用水量(单位:),样本统计结果如图表:| 分组 | 频数 | 频率 |
| [0,1) | a | |
| [1,2) | 0.19 | |
| [2,3) | 50 | b |
| [3,4) | 0.23 | |
| [4,5) | 0.18 | |
| [5,6) | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-3+\sqrt{17},+∞)$ | B. | $(3+\sqrt{17},+∞)$ | C. | $(-3+\sqrt{17},3+\sqrt{17})$ | D. | $(0,-3+\sqrt{17})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2] | B. | $[-\frac{5}{2},+∞)$ | C. | $(-∞,-\frac{5}{2})∪(2,+∞)$ | D. | $(-∞,-\frac{5}{2}]∪[2,+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2ln2 | B. | 2-ln2 | C. | 7-2ln2 | D. | $\frac{15}{2}$-2ln2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com