
【题目】![]() 年,“非典”爆发,以钟南山为代表的医护工作者经长期努力,抗击了非典.
年,“非典”爆发,以钟南山为代表的医护工作者经长期努力,抗击了非典.![]() 年
年![]() 岁高龄的钟院士再次披挂上阵,逆行武汉抗击新冠疫情。为调查中学生对这一伟大“逆行者”的了解程度,某调查小组随机抽取了某市物化生、政史地的
岁高龄的钟院士再次披挂上阵,逆行武汉抗击新冠疫情。为调查中学生对这一伟大“逆行者”的了解程度,某调查小组随机抽取了某市物化生、政史地的![]() 名高中生,请他们列举钟南山院士在医学上的成就,把能列举钟南山成就不少于
名高中生,请他们列举钟南山院士在医学上的成就,把能列举钟南山成就不少于![]() 项的称为“比较了解”,少于三项的称为“不太了解”他们的调查结果如下:
项的称为“比较了解”,少于三项的称为“不太了解”他们的调查结果如下:
组合 | 0项 | 1项 | 2项 | 3项 | 4项 | 5项 | 5项以上 |
物化生(人) | 1 | 10 | 17 | 14 | 14 | 10 | 4 |
政史地(人) | 0 | 8 | 10 | 6 | 3 | 2 | 1 |
(1)请将下面的2×2列联表补充完整;
组合 | 比较了解 | 不太了解 | 合计 |
物化生 | |||
政史地 | |||
合计 |
(2)判断是否有99%的把握认为,了解钟南山与选择物化生、政史地组合有关?
参考:![]()
![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
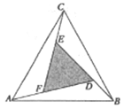
【题目】赵爽是我国古代数学家、天文学家,大约在公元222年,赵爽为《周髀算经》一书作序时,介绍了“勾股圆方图”,亦称“赵爽炫图”(以弦为边长得到的正方形组成).类比“赵爽弦图”,可类似地构造如下图所示的图形,它是由3个全等的三角形与中间的一个小等边三角形拼成的一个大等边三角形,设![]() ,若在大等边三角形中随机取一点,则此点取自小等边三角形的概率是__________.
,若在大等边三角形中随机取一点,则此点取自小等边三角形的概率是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
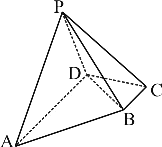
【题目】在四棱锥P-ABCD中,底面ABCD为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,且平面
,且平面![]() 平面ABCD.
平面ABCD.
(1)求证:![]() ;
;
(2)在线段PA上是否存在一点M,使二面角M-BC-D的大小为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若四面体ABCD的三组对棱分别相等,即AB=CD,AC=BD,AD=BC,则下列结论正确的是( )
A.四面体ABCD每组对棱相互垂直
B.四面体ABCD每个面的面积相等
C.从四面体ABCD每个顶点出发的三条棱两两夹角之和大于90°且小于180°
D.连接四面体ABCD每组对棱中点的线段相互垂直平分
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某村电费收取有以下两种方案供农户选择:
方案一:每户每月收取管理费2元,月用电量不超过30度时,每度0.5元;超过30度时,超过部分按每度0.6元收取:
方案二:不收取管理费,每度0.58元.
(1)求方案一的收费L(x)(元)与用电量x(度)间的函数关系.若老王家九月份按方案一缴费35元,问老王家该月用电多少度?
(2)老王家该月用电量在什么范围内,选择方案一比选择方案二好?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,侧面
中,侧面![]() ⊥底面
⊥底面![]() ,底面
,底面![]() 为直角梯形,
为直角梯形,![]() //
//![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.

(Ⅰ)求证:PA//平面BEF;
(Ⅱ)若PC与AB所成角为![]() ,求
,求![]() 的长;
的长;
(Ⅲ)在(Ⅱ)的条件下,求二面角F-BE-A的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com