
| 年 | 第1年 | 第2年 | 第3年 | 第4年 | 第5年 | 第6年 |
| 每池产量 | 1万只 | 1.2万只 | 1.4万只 | 1.6万只 | 1.8万只 | 2万只 |
| 年 | 第1年 | 第2年 | 第3年 | 第4年 | 第5年 | 第6年 |
| 鱼池个数 | 30个 | 26个 | 22个 | 18个 | 14个 | 10个 |
分析 (1)根据图象可知该县第2年甲鱼池的个数,根据由表可知该年平均每个甲鱼池出产甲鱼的只数,从而求出全县出甲鱼的总只数;
(2)根据表可知第1年全县甲鱼只数与第6年全县甲鱼只数,从而得到第6年全县甲鱼总只数比第1年是扩大了还是缩小了;
(3)根据表可知第1年到第6年,每年养甲鱼的个数构成首项为30,公差为-4的等差数列,从而得到第n年养甲鱼池的个数是an=34-4n(n=1,2,…,6),又从第1年到第6年,每个甲鱼池养甲鱼平均只数构成首项为1,公差为0.2的等差数列,从而第n年每个甲鱼池平均养甲鱼池只数是:bn=0.2n+0.8(n=1,2,…,6),因此第n 年全县养甲鱼的总只数Wn=an•bn,再求出最大值和最小值即可.
解答 解:(1)由表可知:该县第2年甲鱼池有26个,该年平均每个甲鱼池出产1.2万只甲鱼,
所以全县共出产1.2×26=31.2(万只甲鱼)…(2分)
(2)依表可知:第1年全县甲鱼1×30=30(万只)
第6年全县甲鱼2×10=20(万只)
因此到第6年全县甲鱼总只数比第1年缩小了…(6分)
(3)依表可知:第1年到第6年,每年甲鱼池的个数构成首项为30,公差为-4的等差数列,
因此第n年甲鱼池的个数是:an=34-4n(n=1,2,…,6)…(8分)
又从第1年到第6年,每个甲鱼池养甲鱼平均只数构成首项为1,公差为0.2的等差数列,
因此第n年每个甲鱼池平均养甲鱼只数是:bn=0.2n+0.8(n=1,2,…,6)…(10分)
因此第n 年全县养甲鱼的总只数Wn=an•bn=(34-4n)(0.2n+0.8)=-0.8n2+3.6n+27.2=-0.8(n-2.25)2+31.25(n=1,2,…,6)…(14分)
可知:当n=2时,即第2年全县养甲鱼为31.2万只,规模最大.…(15分)
显然:W1=30>W6=20,故第6年全县养甲鱼规模最小.…(16分)
点评 本题主要考查了数列的应用和对信息图和表的认识,以及等差数列的通项公式和二次函数的性质,属于中档题.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
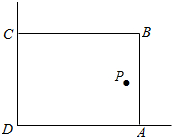 在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两墙足够长),用16m长的篱笆围成一个矩形花园ABCD(篱笆只围AB、BC两边),在P处有一棵树与墙CD、AD的距离分别是a(0<a<12)m和4m,现需要将这棵树围在花园内(含边界,不考虑树的粗细).设矩形ABCD的面积是ym2,长DA为xm.
在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两墙足够长),用16m长的篱笆围成一个矩形花园ABCD(篱笆只围AB、BC两边),在P处有一棵树与墙CD、AD的距离分别是a(0<a<12)m和4m,现需要将这棵树围在花园内(含边界,不考虑树的粗细).设矩形ABCD的面积是ym2,长DA为xm.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | [-1,3] | C. | (-1,1) | D. | (-1,3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com