
【题目】在平面直角坐标系中,曲线![]() 与坐标轴的交点都在圆C上.
与坐标轴的交点都在圆C上.
(1)求圆C的方程;
(2)若圆C与直线![]() 交于A,B两点,且
交于A,B两点,且![]() ,求a的值.
,求a的值.
科目:高中数学 来源: 题型:
【题目】一种密码锁的密码设置是在正![]() 边形
边形![]() 的每个顶点处赋值0和1两个数中的一个,同时,在每个顶点处染红、蓝两种颜色之一,使得任意相邻的两个顶点的数字或颜色中至少有一个相同.问:该种密码锁共有多少种不同的密码设置?
的每个顶点处赋值0和1两个数中的一个,同时,在每个顶点处染红、蓝两种颜色之一,使得任意相邻的两个顶点的数字或颜色中至少有一个相同.问:该种密码锁共有多少种不同的密码设置?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知从境外回国的8位同胞中有1位被新冠肺炎病毒感染,需要通过核酸检测是否呈阳性来确定是否被感染.下面是两种检测方案:
方案一:逐个检测,直到能确定被感染者为止.
方案二:将8位同胞平均分为2组,将每组成员的核酸混合在一起后随机抽取一组进行检测,若检测呈阳性,则表明被感染者在这4位当中,然后逐个检测,直到确定被感染者为止;若检测呈阴性,则在另外一组中逐个进行检测,直到确定被感染者为止.
(1)根据方案一,求检测次数不多于两次的概率;
(2)若每次核酸检测费用都是100元,设方案二所需检测费用为![]() ,求
,求![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】判断下列命题是否正确,请说明理由:
(1)若向量![]() 与
与![]() 同向,且
同向,且![]() ,则
,则![]() ;
;
(2)若向![]() ,则
,则![]() 与
与![]() 的长度相等且方向相同或相反;
的长度相等且方向相同或相反;
(3)对于任意向量![]() ,若
,若![]() 与
与![]() 的方向相同,则
的方向相同,则![]() =
=![]() ;
;
(4)由于![]() 方向不确定,故
方向不确定,故![]() 不与任意向量平行;
不与任意向量平行;
(5)向量![]() 与
与![]() 平行,则向量
平行,则向量![]() 与
与![]() 方向相同或相反.
方向相同或相反.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高中生在被问及“家,朋友聚集的地方,个人空间”三个场所中“感到最幸福的场所在哪里?”这个问题时,从中国某城市的高中生中,随机抽取了55人,从美国某城市的高中生中随机抽取了45人进行答题.中国高中生答题情况是:选择家的占![]() 、朋友聚集的地方占
、朋友聚集的地方占![]() 、个人空间占
、个人空间占![]() .美国高中生答题情况是:朋友聚集的地方占
.美国高中生答题情况是:朋友聚集的地方占![]() 、家占
、家占![]() 、个人空间占
、个人空间占![]() .如下表:
.如下表:
在家里最幸福 | 在其它场所幸福 | 合计 | |
中国高中生 | |||
美国高中生 | |||
合计 |
(Ⅰ)请将![]() 列联表补充完整;试判断能否有
列联表补充完整;试判断能否有![]() 的把握认为“恋家”与否与国别有关;
的把握认为“恋家”与否与国别有关;
(Ⅱ)从被调查的不“恋家”的美国学生中,用分层抽样的方法选出4人接受进一步调查,再从4人中随机抽取2人到中国交流学习,求2人中含有在“个人空间”感到幸福的学生的概率.
附:![]() ,其中
,其中![]() .
.
| 0.050 | 0.025 | 0.010 | 0.001 |
| 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为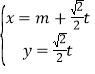 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,椭圆
轴正半轴为极轴建立极坐标系,椭圆![]() 的极坐标方程为
的极坐标方程为![]() ,其左焦点
,其左焦点![]() 在直线
在直线![]() 上.
上.
(1)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,求
两点,求![]() 的值;
的值;
(2)求椭圆![]() 的内接矩形面积的最大值.
的内接矩形面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() 是曲线
是曲线![]() 上的动点,求点
上的动点,求点![]() 到曲线
到曲线![]() 的最小距离.
的最小距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个特定时段内,以点E为中心的7n mile以内海域被设为警戒水域.点E正北55n mile处有一个雷达观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°且与点A相距40![]() n mile的位置B,经过40分钟又测得该船已行驶到点A北偏东
n mile的位置B,经过40分钟又测得该船已行驶到点A北偏东![]() (其中
(其中![]() ,
,![]() )且与点A相距10
)且与点A相距10![]() n mile的位置C.
n mile的位置C.
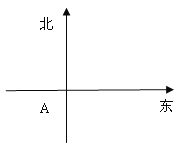
(I)求该船的行驶速度(单位:n mile /h);
(II)若该船不改变航行方向继续行驶.判断它是否会进入警戒水域,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确命题的个数是( )
(1)若函数![]() 的定义域
的定义域![]() 关于原点对称,则
关于原点对称,则![]() 为偶函数的充要条件为对任意的
为偶函数的充要条件为对任意的![]() ,
,![]() 都成立;
都成立;
(2)若函数![]() 的定义域
的定义域![]() 关于原点对称,则“
关于原点对称,则“![]() ”是“
”是“![]() 为奇函数”的必要条件;
为奇函数”的必要条件;
(3)函数![]() 对任意的实数
对任意的实数![]() 都有
都有![]() ,则
,则![]() 在实数集
在实数集![]() 上是增函数;
上是增函数;
(4)已知函数![]() 在其定义域内有两个不同的极值点,则实数
在其定义域内有两个不同的极值点,则实数![]() 的取值范围是
的取值范围是![]() .
.
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com