
分析 由题意知f(2×2)=f(2)+f(2)=2,f(2×4)=f(2)+f(4)=3,f(x)>f(8x-16),再由f(x)的定义域为(0,+∞),且在其上为增函数得得到不等式组,即可解得答案.
解答 解:∵f(xy)=f(x)+f(y),f(3)=1,
∴f(3×3)=f(3)+f(3)=2,
f(3×9)=f(3)+f(9)=3,
∵f(x)-f(x-2)>3,
∴f(x)>f(x-2)+f(27)=f(27x-54)
∵f(x)是定义在(0,+∞)上的增函数解得,
$\left\{\begin{array}{l}x>0\\ x-2>0\\ x>27x-54\end{array}\right.$
解得,2<x<$\frac{27}{13}$.
所以不等式f(x)-f(x-2)<3的解集为(2,$\frac{27}{13}$).
故答案为:(2,$\frac{27}{13}$).
点评 本题考查了抽象函数及其应用,函数的性质和应用,解题时要认真审题,仔细解答.


科目:高中数学 来源: 题型:选择题
| A. | 45 | B. | 46 | C. | 47 | D. | 48 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x1)<0,f(x2)<0 | B. | f(x1)<0,f(x2)>0 | C. | f(x1)>0,f(x2)<0 | D. | f(x1)>0,f(x2)>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | $\sqrt{3}$+2 | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
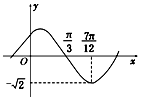 (1)求$f(x)=tan(3x-\frac{π}{4})$的定义域
(1)求$f(x)=tan(3x-\frac{π}{4})$的定义域查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
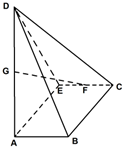 已知底面为矩形的四棱锥D-ABCE,AB=1,BC=2,AD=3,DE=$\sqrt{5}$,DE⊥AE,G、F分别为AD,CE的中点,其中二面角D-AE-C的平面角的正切值为-tan2.
已知底面为矩形的四棱锥D-ABCE,AB=1,BC=2,AD=3,DE=$\sqrt{5}$,DE⊥AE,G、F分别为AD,CE的中点,其中二面角D-AE-C的平面角的正切值为-tan2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com