
分析 (1)先将条件p,q化简,然后利用p是q的充分不必要条件,确定参数a的取值范围;(2)先求出关于p,q为真命题时的a的范围,通过讨论p,q的真假,从而求出a的范围.
解答 解:(1)命题p:(x+2)(x-10)≤0,
∴-2≤x≤10,
命题q:1-m≤x≤1+m,m>0
∴1-m≤x≤1+m,
∵q是p的充分不必要条件,
p:x∈[-2,10],q:x∈[1-m,1+m]
∴[1-m,1+m]?[-2,10],
∴$\left\{\begin{array}{l}{1-m>-2}\\{1+m<10}\end{array}\right.$,解得:$\left\{\begin{array}{l}{m<3}\\{m<9}\end{array}\right.$,
当1-m=-2时,m=3,
[-2,4]?[-2,10],
∴m=3成立,
∴实数m的取值范围是[3,+∞);
(2)若命题p:|a|<2,
则-2<a<2,
命题q:一次函数f(x)=(2-2a)x+1是增函数,
则2-2a>0,解得:a<1,
若p∨q为真,p∧q为假,
则p,q一真一假,
p真q假时:$\left\{\begin{array}{l}{-2<a<2}\\{a≥1}\end{array}\right.$,解得:1≤a<2,
p假q真时:$\left\{\begin{array}{l}{a≥2或a≤-2}\\{a<1}\end{array}\right.$,解得:a≤-2,
综上:a∈(-∞,-2]∪[1,2).
点评 本题考查了复合命题的判断,考查充分必要条件,是一道中档题.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 关于x轴对称 | B. | 关于y轴对称 | C. | 关于原点对称 | D. | 关于直线y=x对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
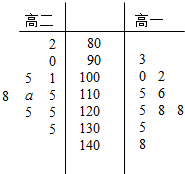 高三学生小周把自己在高二时的10次数学考试成绩和高三时的10次数学考试成绩(试卷总分150分)进行统计,统计数据用茎叶图表示(如图所示)
高三学生小周把自己在高二时的10次数学考试成绩和高三时的10次数学考试成绩(试卷总分150分)进行统计,统计数据用茎叶图表示(如图所示)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 角α和β的顶点为平面直角坐标系的原点,始边都与x轴的正半轴重合,终边分别与单位圆(半径为1)相交于点P、Q两点,已知Q点也在射线y=-$\frac{4}{3}$x(x<0)上.
角α和β的顶点为平面直角坐标系的原点,始边都与x轴的正半轴重合,终边分别与单位圆(半径为1)相交于点P、Q两点,已知Q点也在射线y=-$\frac{4}{3}$x(x<0)上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com