
分析 (1)$({\begin{array}{l}0&1\\ 1&0\end{array}})({\begin{array}{l}2\\ 3\end{array}})=({\begin{array}{l}3\\ 2\end{array}})$,即可得出结论;
(2)在曲线x2+4xy+2y2=1上任取一点(m,n),则$({\begin{array}{l}1&a\\ b&1\end{array}})({\begin{array}{l}m\\ n\end{array}})=({\begin{array}{l}m+an\\ bm+n\end{array}})$,将(m+an,bm+n)代入x2-2y2=1,由此能求出a,b的值.
解答 解:(1)$({\begin{array}{l}0&1\\ 1&0\end{array}})({\begin{array}{l}2\\ 3\end{array}})=({\begin{array}{l}3\\ 2\end{array}})$,所以点(2,3)在$({\begin{array}{l}0&1\\ 1&0\end{array}})$的作用下变成点(3,2).
(2)在曲线x2+4xy+2y2=1上任取一点(m,n),
则$({\begin{array}{l}1&a\\ b&1\end{array}})({\begin{array}{l}m\\ n\end{array}})=({\begin{array}{l}m+an\\ bm+n\end{array}})$,将(m+an,bm+n)代入x2-2y2=1,
得(m+an)2-2(bm+n)2=1,
即(1-2b2)m2+2(a-2b)mn+(a2-2)n2=1.
又点(m,n)在曲线x2+4xy+2y2=1上,所以m2+4mn+2n2=1.
前面两个式子对照,由待定系数法可知:$\left\{\begin{array}{l}1-2{b^2}=1\\ 2(a-2b)=4\\{a^2}-2=2\end{array}\right.$,
解得$\left\{{\begin{array}{l}a=2\\ b=0\end{array}}\right.$,所以a+b=2.
点评 本题以矩阵为载体,考查矩阵的乘法,考查矩阵变换的应用.解题时要认真审题,仔细解答.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | [-2,0) | C. | [0,2] | D. | {0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x-1)2+(y+1)2=9 | B. | (x-1)2+(y+1)2=3 | C. | (x+1)2+(y-1)2=9 | D. | (x+1)2+(y-1)2=3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
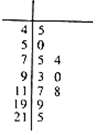 空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数,空气质量按照AQI大小分为六级,0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~250为重度污染;>300为严重污染.一环保人士记录2017年某地某月10天的AQI的茎叶图如图.
空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数,空气质量按照AQI大小分为六级,0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~250为重度污染;>300为严重污染.一环保人士记录2017年某地某月10天的AQI的茎叶图如图.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | P(X=0) | B. | P(X≤2) | C. | P(X=1) | D. | P(X=2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com