
【题目】如图,在长方体ABCD﹣A1B1C1D1中,AB=2BB1=2BC,E为D1C1的中点,连结ED,EC,EB和DB.
(Ⅰ)证明:A1D1∥平面EBC;
(Ⅱ)证明:平面EDB⊥平面EBC.
【答案】证明:(Ⅰ)在长方体ABCD﹣A1B1C1D1中,
∴A1D1∥AD∥BC
∵A1D1∥BC,A1D1平面EBC,BC平面EBC
∴A1D1∥平面EBC
(Ⅱ)BB1=BC=a则AB=2a且 ![]() ,∴DE2+EC2=4a2=DC2 , ∴DE⊥EC…(10分)
,∴DE2+EC2=4a2=DC2 , ∴DE⊥EC…(10分) ![]() ,DB2=DC2+BC2=5a2 ,
,DB2=DC2+BC2=5a2 ,
又ED2=2a2 , ∴DE2+EB2=DB2 , ∴DE⊥EB
所以DE⊥平面EBC,DE平面EBD
所以平面EDB⊥平面EBC
【解析】(Ⅰ)证明:A1D1∥BC,即可证明A1D1∥平面EBC;(Ⅱ)证明:DE⊥平面EBC,即可证明平面EDB⊥平面EBC.
【考点精析】利用直线与平面平行的判定和平面与平面垂直的判定对题目进行判断即可得到答案,需要熟知平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一个平面过另一个平面的垂线,则这两个平面垂直.


科目:高中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() ),焦点
),焦点![]() 到准线的距离为
到准线的距离为![]() ,过点
,过点![]()
![]() 作直线
作直线![]() 交抛物线
交抛物线![]() 于点
于点![]() (点
(点![]() 在第一象限).
在第一象限).
(Ⅰ)若点![]() 焦点
焦点![]() 重合,且弦长
重合,且弦长![]() ,求直线
,求直线![]() 的方程;
的方程;
(Ⅱ)若点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,直线
,直线![]() 交x轴于点
交x轴于点![]() ,且
,且![]() ,求证:点B的坐标是
,求证:点B的坐标是![]() ,并求点
,并求点![]() 到直线
到直线![]() 的距离
的距离![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大学生赵敏利用寒假参加社会实践,对机械销售公司7月份至12月份销售某种机械配件的销售量及销售单价进行了调查,销售单价![]() 和销售量
和销售量![]() 之间的一组数据如下表所示:
之间的一组数据如下表所示:
月份 | 7 | 8 | 9 | 10 | 11 | 12 |
销售单价 | 9 | 9.5 | 10 | 10.5 | 11 | 8 |
销售量 | 11 | 10 | 8 | 6 | 5 | 14 |
(1)根据7至11月份的数据,求出![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过0.5元,则认为所得到的回归直线方程是理想的,试问(1)中所得到的回归直线方程是否理想?
(3)预计在今后的销售中,销售量与销售单价仍然服从(1)中的关系,若该种机器配件的成本是2.5元/件,那么该配件的销售单价应定为多少元才能获得最大利润?(注:利润=销售收入-成本).
参考公式:回归直线方程![]() ,其中
,其中 ,参考数据:
,参考数据: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若钝角三角形的三边长和面积都是整数,则称这样的三角形为“钝角整数三角形”,下列选项中能构成一个“钝角整数三角形”三边长的是( )
A.2,3,4
B.2,4,5
C.5,5,6
D.4,13,15
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 满足3an﹣2Sn﹣1=0.
(1)求数列{an}的通项公式;
(2)bn= ![]() ,数列{bn}的前n项和为Tn , 求f(n)=
,数列{bn}的前n项和为Tn , 求f(n)= ![]() (n∈N+)的最大值.
(n∈N+)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)曲线![]() 与
与![]() 相交于
相交于![]() 两点,求过
两点,求过![]() 两点且面积最小的圆的标准方程.
两点且面积最小的圆的标准方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市有大型超市200家、中型超市400家、小型超市1400 家.为掌握各类超市的营业情况,现按分层抽样方法抽取一个容量为100的样本,应抽取中型超市( )
A.70家
B.50家
C.20家
D.10家
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图,估计这次测试中数学成绩的平均分、众数、中位数分别是( ) 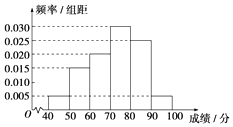
A.73.3,75,72
B.72,75,73.3
C.75,72,73.3
D.75,73.3,72
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:若x>0,则函数y=x+ ![]() 的最小值为1,命题q:若x>1,则x2+2x﹣3>0,则下列命题是真命题的是( )
的最小值为1,命题q:若x>1,则x2+2x﹣3>0,则下列命题是真命题的是( )
A.p∨q
B.p∧q
C.(¬p)∧(¬q)
D.p∨(¬q)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com