
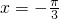 对称,则a的值为
对称,则a的值为 ;
;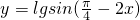 的单调增区间是
的单调增区间是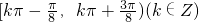 ;
;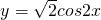 的图象向左平移
的图象向左平移 个单位;
个单位;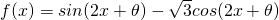 是偶函数且在
是偶函数且在 上是减函数的θ的一个可能值是
上是减函数的θ的一个可能值是 .其中正确命题的个数是
.其中正确命题的个数是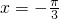 对称,则f(
对称,则f( )=±
)=± ,
, )+acos(
)+acos( )=
)= ,解之得a=
,解之得a= ,故①正确;
,故①正确;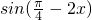 >0,所以函数的定义域为:{x|kπ-
>0,所以函数的定义域为:{x|kπ- <x<kπ+
<x<kπ+ },
},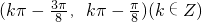 ,故②不正确;
,故②不正确; sin60°=
sin60°= ,q=sin16°+cos16°=
,q=sin16°+cos16°= sin61°
sin61°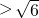 ,
,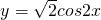 的图象向左平移
的图象向左平移 个单位得到
个单位得到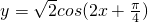 的图象;
的图象; cos(2x+
cos(2x+ ),所以④正确;
),所以④正确; 时,函数
时,函数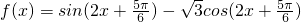 =2sin(2x+
=2sin(2x+ )=2cos2x,
)=2cos2x, 上是减函数且为偶函数,故⑤正确.
上是减函数且为偶函数,故⑤正确.

科目:高中数学 来源: 题型:
| π |
| 6 |
| π |
| 3 |
| 1 |
| f(x) |
| OA |
| OB |
| CO |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源:2011年四川省绵阳中学高考适应性检测数学试卷(理科)(解析版) 题型:填空题
 ”是“|2y-x|≤2”的充分不必要条件.
”是“|2y-x|≤2”的充分不必要条件.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
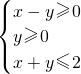 ”是“|2y-x|≤2”的充分不必要条件.
”是“|2y-x|≤2”的充分不必要条件.查看答案和解析>>
科目:高中数学 来源:2010年山东省高考数学模拟试卷1(文科)(解析版) 题型:解答题
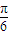 )图象的一个对称中心为点(
)图象的一个对称中心为点(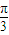 ,0);③若函数f(x)在R上满足f(x+1)=
,0);③若函数f(x)在R上满足f(x+1)=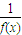 ,则f(x)是周期为2的函数;④在△ABC中,若
,则f(x)是周期为2的函数;④在△ABC中,若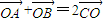 ,则S△ABC=S△BOC其中正确命题的序号为 .
,则S△ABC=S△BOC其中正确命题的序号为 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com