
【题目】定义域和值域均为[-a,a]的函数y=![]() 和y=g(x)的图象如图所示,其中a>c>b>0,给出下列四个结论正确结论的是( )
和y=g(x)的图象如图所示,其中a>c>b>0,给出下列四个结论正确结论的是( )
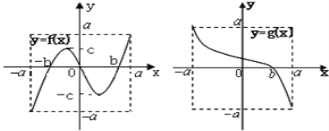
A.方程f[g(x)]=0有且仅有三个解B.方程g[f(x)]=0有且仅有三个解
C.方程f[f(x)]=0有且仅有九个解D.方程g[g(x)]=0有且仅有一个解
【答案】AD
【解析】
根据给定的函数的图象,结合函数的单调性,逐项判定,即可求解,得到答案。
由图象可知对于函数![]() ,当
,当![]() 时,方程有一解,当
时,方程有一解,当![]() 时,方程有两解,当
时,方程有两解,当![]() 时方程由三解,当
时方程由三解,当![]() 时,方程有两解,当
时,方程有两解,当![]() 时,方程有一解,对于函数
时,方程有一解,对于函数![]() ,由图象可知,函数
,由图象可知,函数![]() 为单调递减函数,当
为单调递减函数,当![]() ,方程有唯一解。
,方程有唯一解。
对于A中,设![]() ,则由
,则由![]() ,即
,即![]() ,此时方程有三个
,此时方程有三个![]() 的值,即
的值,即![]() 有三个不同的值,又由函数
有三个不同的值,又由函数![]() 为单调递减函数,所以方程
为单调递减函数,所以方程![]() 有三个不同的解,所以是正确的;
有三个不同的解,所以是正确的;
对于B中,设![]() ,则由
,则由![]() ,即
,即![]() ,此时只有唯一的解
,此时只有唯一的解![]() ,即方程
,即方程![]() ,此时可能有一解、两解或三解,所以不正确;
,此时可能有一解、两解或三解,所以不正确;
对于C中,设![]() ,则由
,则由![]() ,即
,即![]() ,此时
,此时![]() 或
或![]() 或
或![]() ,
,
则方程![]() 可能有5个解或7个解,或9个解,所以不正确;
可能有5个解或7个解,或9个解,所以不正确;
对于D中,设![]() ,则由
,则由![]() ,即
,即![]() ,此时
,此时![]() ,对于方程
,对于方程![]() ,只有唯一的解,所以是正确的。
,只有唯一的解,所以是正确的。
故选:AD。


科目:高中数学 来源: 题型:
【题目】某地最近十年粮食需求量逐年上升,下表是部分统计数据
![]()
(1)利用所给数据求年需求量与年份之间的回归直线方程![]() ;
;
(2)利用(1)计算2002年和2006年粮食需求量的残差;
(3)利用(1)中所求出的直线方程预测该地2012年的粮食需求量。
公式:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,其可见部分如图所示.据此解答如下问题:
(1)计算频率分布直方图中[80,90)间的矩形的高;
(2)根据茎叶图和频率分布直方图估计这次测试的平均分.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为鼓励大学毕业生自主创业,某市出台了相关政策:由政府协调,企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.某大学毕业生按照相关政策投资销售一种新型节能灯.已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月的销售量y(单位:件)与销售单价x(单位:元)之间的关系近似满足一次函数:![]() .
.
(1)设他每月获得的利润为w(单位:元),写出他每月获得的利润w与销售单价x的函数关系.
(2)相关部门规定,这种节能灯的销售单价不得高于25元.如果他想要每月获得的利润不少于3000元,那么政府每个月为他承担的总差价的取值范围是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次考试中某班级50名学生的成绩统计如表,规定75分以下为一般,大于等于75分小于85分为良好,85分及以上为优秀.
![]()
经计算样本的平均值![]() ,标准差
,标准差![]() . 为评判该份试卷质量的好坏,从其中任取一人,记其成绩为
. 为评判该份试卷质量的好坏,从其中任取一人,记其成绩为![]() ,并根据以下不等式进行评判
,并根据以下不等式进行评判
① ![]() ;
;
② ![]() ;
;
③ ![]()
评判规则:若同时满足上述三个不等式,则被评为优秀试卷;若仅满足其中两个不等式,则被评为合格试卷;其他情况,则被评为不合格试卷.
(1)试判断该份试卷被评为哪种等级;
(2)按分层抽样的方式从3个层次的学生中抽出10名学生,再从抽出的10名学生中随机抽出4人进行学习方法交流,用随机变量![]() 表示4人中成绩优秀的人数,求随机变量
表示4人中成绩优秀的人数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com