
【题目】设抛物线![]() 的焦点为
的焦点为![]() ,过点
,过点![]() 作直线
作直线![]() 与抛物线交于
与抛物线交于![]() ,
,![]() 两点,点
两点,点![]() 满足
满足![]() ,过
,过![]() 作
作![]() 轴的垂线与抛物线交于点
轴的垂线与抛物线交于点![]() ,若
,若![]() ,则点
,则点![]() 的横坐标为__________,
的横坐标为__________,![]() __________.
__________.
【答案】1 8
【解析】
利用抛物线的定义,求得![]() 点的坐标,设出直线
点的坐标,设出直线![]() 的方程,联立直线的方程和抛物线的方程,利用韦达定理,求得
的方程,联立直线的方程和抛物线的方程,利用韦达定理,求得![]() 点坐标的表达式,根据
点坐标的表达式,根据![]() 两点的纵坐标相同列方程,解方程求得直线
两点的纵坐标相同列方程,解方程求得直线![]() 的斜率,由此求得
的斜率,由此求得![]() .
.
由于点![]() 满足
满足![]() ,所以
,所以![]() 是线段
是线段![]() 的中点.抛物线的焦点坐标为
的中点.抛物线的焦点坐标为![]() ,准线方程为
,准线方程为![]() .设
.设![]() ,由于
,由于![]() 在抛物线上,且
在抛物线上,且![]() ,根据抛物线的定义得
,根据抛物线的定义得![]() ,所以
,所以![]() ,则
,则![]() ,不妨设
,不妨设![]() .若直线
.若直线![]() 斜率不存在,则
斜率不存在,则![]() ,则
,则![]() ,此时
,此时![]() 的纵坐标和
的纵坐标和![]() 的纵坐标不相同,不符合题意.所以直线
的纵坐标不相同,不符合题意.所以直线![]() 的斜率存在.设
的斜率存在.设![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,代入抛物线方程并化简得
,代入抛物线方程并化简得![]() ,则
,则![]() .由于
.由于![]() 是线段
是线段![]() 中点,所以
中点,所以![]() ,而
,而![]() ,所以
,所以![]() ,即
,即![]() ,即
,即![]() ,解得
,解得![]() .所以
.所以![]() ,所以
,所以![]() ,则
,则![]() 到准线
到准线![]() 的距离为
的距离为![]() ,根据抛物线的定义结合中位线的性质可知
,根据抛物线的定义结合中位线的性质可知![]() .
.
故答案为:(1). 1 (2). 8


科目:高中数学 来源: 题型:
【题目】已知![]()
![]() 分别是双曲线
分别是双曲线![]()
![]() 的左、右焦点,A为左顶点,P为双曲线右支上一点,若
的左、右焦点,A为左顶点,P为双曲线右支上一点,若![]() 且
且![]() 的最小内角为
的最小内角为![]() ,则( )
,则( )
A.双曲线的离心率![]() B.双曲线的渐近线方程为
B.双曲线的渐近线方程为![]()
C.![]() D.直线
D.直线![]() 与双曲线有两个公共点
与双曲线有两个公共点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解春季昼夜温差大小与某种子发芽多少之间的关系,现在从4月份的30天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每100颗种子浸泡后的发芽数,得到如下表格:
日期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
温差x/oC | 10 | 11 | 13 | 12 | 8 |
发芽数y/颗 | 23 | 25 | 30 | 26 | 16 |
(Ⅰ)从这5天中任选2天,若选取的是4月1日与4月30日的两组数据,请根据这5天中的另3天的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]()
(Ⅱ)若由线性回归方程得到的估计数据与所选出的两组检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠.
(参考公式, 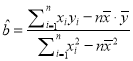 ,
, ![]() ),参考数据
),参考数据![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“悦跑圈”是一款基于社交型的跑步应用,用户通过该平台可查看自己某时间段的运动情况,某人根据![]() 年
年![]() 月至
月至![]() 年
年![]() 月期间每月跑步的里程(单位:十公里)的数据绘制了下面的折线图,根据该折线图,下 列结论正确的是( )
月期间每月跑步的里程(单位:十公里)的数据绘制了下面的折线图,根据该折线图,下 列结论正确的是( )
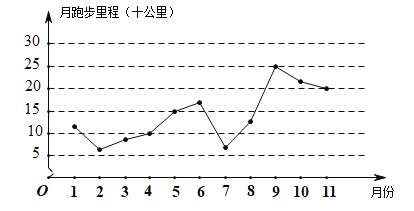
A.月跑步里程逐月增加
B.月跑步里程最大值出现在![]() 月
月
C.月跑步里程的中位数为![]() 月份对应的里程数
月份对应的里程数
D.![]() 月至
月至![]() 月的月跑步里程相对于
月的月跑步里程相对于![]() 月至
月至![]() 月波动性更小,变化比较平稳
月波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为F,点
的焦点为F,点![]() 在此抛物线上,
在此抛物线上,![]() ,不过原点的直线
,不过原点的直线![]() 与抛物线C交于A,B两点,以AB为直径的圆M过坐标原点.
与抛物线C交于A,B两点,以AB为直径的圆M过坐标原点.
(1)求抛物线C的方程;
(2)证明:直线![]() 恒过定点;
恒过定点;
(3)若线段AB中点的纵坐标为2,求此时直线![]() 和圆M的方程.
和圆M的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义![]() ,
,![]() ,…,
,…,![]() 的“倒平均数”为
的“倒平均数”为![]() .
.
(1)若数列![]() 前
前![]() 项的“倒平均数”为
项的“倒平均数”为![]() ,求
,求![]() 的通项公式;
的通项公式;
(2)设数列![]() 满足:当
满足:当![]() 为奇数时,
为奇数时,![]() ,当
,当![]() 为偶数时,
为偶数时,![]() .若
.若![]() 为
为![]() 前
前![]() 项的倒平均数,求
项的倒平均数,求![]() ;
;
(3)设函数![]() ,对(1)中的数列
,对(1)中的数列![]() ,是否存在实数
,是否存在实数![]() ,使得当
,使得当![]() 时,
时,![]() 对任意
对任意![]() 恒成立?若存在,求出最大的实数
恒成立?若存在,求出最大的实数![]() ;若不存在,说明理由.
;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,
,![]() 为左焦点,
为左焦点,![]() 为上顶点,
为上顶点,![]() 为右顶点,若
为右顶点,若![]() ,抛物线
,抛物线![]() 的顶点在坐标原点,焦点为
的顶点在坐标原点,焦点为![]() .
.
(1)求![]() 的标准方程;
的标准方程;
(2)是否存在过![]() 点的直线,与
点的直线,与![]() 和
和![]() 交点分别是
交点分别是![]() 和
和![]() ,使得
,使得![]() ?如果存在,求出直线的方程;如果不存在,请说明理由.
?如果存在,求出直线的方程;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着中国教育改革的不断深入,越来越多的教育问题不断涌现.“衡水中学模式”入驻浙江,可以说是应试教育与素质教育的强烈碰撞.这一事件引起了广大市民的密切关注.为了了解广大市民关注教育问题与性别是否有关,记者在北京,上海,深圳随机调查了100位市民,其中男性55位,女性45位.男性中有45位关注教育问题,其余的不关注教育问题;女性中有30位关注教育问题,其余的不关注教育问题.
(1)根据以上数据完成下列2×2列联表;
关注教育问题 | 不关注教育问题 | 合计 | |||||
女 | 30 | 45 | |||||
男 | 45 | 55 | |||||
合计 |
| 100 | |||||
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | ||
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | ||
(2)能否在犯错误的概率不超过0.025的前提下认为是否关注教育与性别有关系?
参考公式: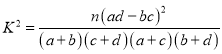 ,其中
,其中![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com