解:(1)∵e=

,不妨设c=3k,a=5k,则b=4k,其中k>0,故椭圆方程为
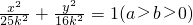
,
∵P(4,

)在椭圆上,∴
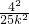
+
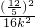
=1,解得k=1,
∴椭圆方程为

+

=1;
(2)K
AP=
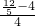
=-

,则直线AP的方程为y=-

x+4,
令y=t(0<t<4),则x=

(4-t),∴M(
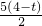
,t),∵Q(0,t)∴N(
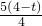
,t),
∵圆N与x轴相切,∴
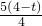
=t,由题意M为第一象限的点,则由
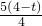
=t,解得t=

,
∴N(

,

),
∴圆N的方程为
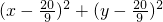
=
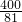
;
(3)F(3,0),k
AP=

,∴直线PF的方程为y=

(x-3),即12x-5y-36=0,
∴点N到直线PF的距离为
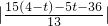
=
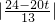
=
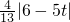
,
∴d=
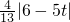
+

(4-t),∵0<t<4,
∴当0<t≤

时,d=
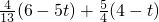
=
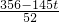
,此时
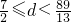
,
当

<t<4时,d=
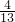
(5t-6)+

(4-t)=
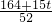
,此时
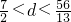
,
∴综上,d的取值范围为[

,
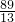
).
分析:(1)由e=

,不妨设c=3k,a=5k,则b=4k,其中k>0,从而可得椭圆方程,把点P坐标代入椭圆方程即可求得k值,进而得椭圆方程;
(2)由点斜式可得直线AP的方程为y=-

x+4,通过解方程可得M,N坐标,圆N与x轴相切可得半径为t,从而可求得t值,进而可求得圆N方程;
(3)点R到直线PF的最大距离为d等于圆心N到直线PF的距离加上半径,根据d的表达式分类讨论即可求得其范围;
点评:本题考查直线与圆锥曲线的位置关系及椭圆标准方程的求解,考查分类讨论思想,考查学生分析解决问题的能力,熟练求解直线方程、熟记点到直线的距离公式等是解决相关问题的基础.

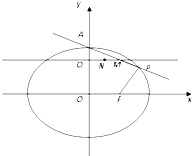 已知椭圆
已知椭圆 的离心率为
的离心率为 ,且过点P(4,
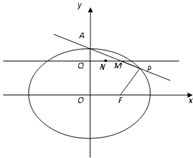
,且过点P(4, ),A为上顶点,F为右焦点.点Q(0,t)是线段OA(除端点外)上的一个动点,过Q作平行于x轴的直线交直线AP于点M,以QM为直径的圆的圆心为N.
),A为上顶点,F为右焦点.点Q(0,t)是线段OA(除端点外)上的一个动点,过Q作平行于x轴的直线交直线AP于点M,以QM为直径的圆的圆心为N. ,不妨设c=3k,a=5k,则b=4k,其中k>0,故椭圆方程为
,不妨设c=3k,a=5k,则b=4k,其中k>0,故椭圆方程为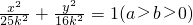 ,
, )在椭圆上,∴
)在椭圆上,∴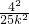 +
+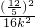 =1,解得k=1,
=1,解得k=1, +
+ =1;
=1;
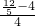 =-
=- ,则直线AP的方程为y=-
,则直线AP的方程为y=- x+4,
x+4, (4-t),∴M(
(4-t),∴M(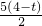 ,t),∵Q(0,t)∴N(
,t),∵Q(0,t)∴N(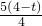 ,t),
,t),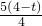 =t,由题意M为第一象限的点,则由
=t,由题意M为第一象限的点,则由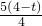 =t,解得t=
=t,解得t= ,
, ,
, ),
),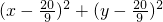 =
=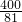 ;
; ,∴直线PF的方程为y=
,∴直线PF的方程为y= (x-3),即12x-5y-36=0,
(x-3),即12x-5y-36=0,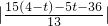 =
=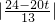 =
=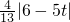 ,
,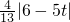 +
+ (4-t),∵0<t<4,
(4-t),∵0<t<4, 时,d=
时,d=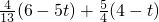 =
=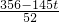 ,此时
,此时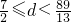 ,
, <t<4时,d=
<t<4时,d=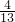 (5t-6)+
(5t-6)+ (4-t)=
(4-t)=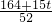 ,此时
,此时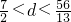 ,
, ,
,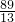 ).
). ,不妨设c=3k,a=5k,则b=4k,其中k>0,从而可得椭圆方程,把点P坐标代入椭圆方程即可求得k值,进而得椭圆方程;
,不妨设c=3k,a=5k,则b=4k,其中k>0,从而可得椭圆方程,把点P坐标代入椭圆方程即可求得k值,进而得椭圆方程; x+4,通过解方程可得M,N坐标,圆N与x轴相切可得半径为t,从而可求得t值,进而可求得圆N方程;
x+4,通过解方程可得M,N坐标,圆N与x轴相切可得半径为t,从而可求得t值,进而可求得圆N方程;

 如图,在由圆O:x2+y2=1和椭圆C:
如图,在由圆O:x2+y2=1和椭圆C: 如图,A,B是椭圆C:
如图,A,B是椭圆C: