
【题目】已知函数![]() ,
, ![]() .
.
(1)求证:对![]() ,函数
,函数![]() 与
与![]() 存在相同的增区间;
存在相同的增区间;
(2)若对任意的![]() ,
, ![]() ,都有
,都有![]() 成立,求正整数
成立,求正整数![]() 的最大值.
的最大值.
【答案】(1)见解析(2)4
【解析】试题分析: ![]() 对
对![]() 求导,求出函数的增区间,对
求导,求出函数的增区间,对![]() 求导,讨论当
求导,讨论当![]() 时、当
时、当![]() 时两种情况的增区间,得证(2)构造
时两种情况的增区间,得证(2)构造![]()
![]() ,将其转化为关于
,将其转化为关于![]() 的一元二次不等式,结合题意
的一元二次不等式,结合题意![]() 化简得
化简得![]() ,然后求导解不等式
,然后求导解不等式
解析:(1)![]() ,所以
,所以![]() 在
在![]() 为增函数,在
为增函数,在![]() 为减函数,
为减函数,
由![]()
![]() ,
,
当![]() 时,
时, ![]() 恒成立,则
恒成立,则![]() 在
在![]() 上单调递增,所以命题成立,
上单调递增,所以命题成立,
当![]() 时,
时, ![]() 在
在![]() 为减函数,在
为减函数,在![]() 为增函数,
为增函数,
设![]() 得
得![]() ,令
,令![]() 得
得![]() ,
,
![]() 在
在![]() 为减函数,在
为减函数,在![]() 为增函数,且
为增函数,且![]() ,所以
,所以![]() ,
,
同理![]() ,所以
,所以![]() ,所以
,所以![]() 与
与![]() 存在相同的增区间.
存在相同的增区间.
综上:命题成立.
(2)证明:对任意的![]() ,
, ![]() ,都有
,都有![]() ,
,
则![]()
![]()
![]() ,
,
则![]()
![]() ,所以
,所以![]()
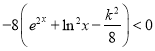 ,
,
则![]() ,由(1)可知
,由(1)可知![]() ,所以有:
,所以有: ![]() 恒成立.
恒成立.
设![]() ,则
,则![]() ,且
,且![]() ,
,
由![]() ,
, ![]()
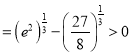 ,
,
所以![]() 在
在![]() 上有唯一实数根
上有唯一实数根![]() ,且
,且![]() ,
,
当![]() 时
时![]() 为减函数,当
为减函数,当![]() 时
时![]() 为增函数,
为增函数,
所以, ![]()
![]() ,
, ![]() ,所以
,所以![]() ,
,
![]() 且
且![]() 是正整数,所以
是正整数,所以![]() ,所以
,所以![]() 的最大值为4.
的最大值为4.


科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象与
的图象与![]() 轴的交点为
轴的交点为![]() ,它在
,它在![]() 轴右侧的第一个最高点和第一个最低点的坐标分别为
轴右侧的第一个最高点和第一个最低点的坐标分别为![]() 和
和![]() .
.
(1)求![]() 解析式及
解析式及![]() 的值;
的值;
(2)求![]() 的单调增区间;
的单调增区间;
(3)若![]() 时,函数
时,函数![]() 有两个零点,求实数
有两个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
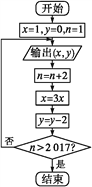
【题目】已知某算法的程序框图如图所示,若将输出的(x,y)值依次记为(x1,y1),(x2,y2),…,(xn,yn),…
(1)若程序运行中输出的一个数组是(9,t),求t的值.
(2)程序结束时,共输出(x,y)的组数为多少?
(3)写出程序框图的程序语句.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司2016年前三个月的利润(单位:百万元)如下:
月份 | 1 | 2 | 3 |
利润 | 2 | 3.9 | 5.5 |
(1)求利润![]() 关于月份
关于月份![]() 的线性回归方程;
的线性回归方程;
(2)试用(1)中求得的回归方程预测4月和5月的利润;
(3)试用(1)中求得的回归方程预测该公司2016年从几月份开始利润超过1000万?
相关公式: .
.
【答案】(1)![]() ;(2)905万;(3)6月
;(2)905万;(3)6月
【解析】试题(1)根据平均数和最小二乘法的公式,求解![]() ,求出
,求出![]() ,即可求解回归方程;(2)把
,即可求解回归方程;(2)把![]() 和
和![]() 分别代入,回归直线方程,即可求解;(3)令
分别代入,回归直线方程,即可求解;(3)令![]() ,即可求解
,即可求解![]() 的值,得出结果.
的值,得出结果.
试题解析:(1)![]() ,
, ,
,![]() ,
,
故利润![]() 关于月份
关于月份![]() 的线性回归方程
的线性回归方程![]() .
.
(2)当![]() 时,
时,![]() ,故可预测
,故可预测![]() 月的利润为
月的利润为![]() 万.
万.
当![]() 时,
时,![]() , 故可预测
, 故可预测![]() 月的利润为
月的利润为![]() 万.
万.
(3)由![]() 得
得![]() ,故公司2016年从
,故公司2016年从![]() 月份开始利润超过
月份开始利润超过![]() 万.
万.
考点:1、线性回归方程;2、平均数.
【题型】解答题
【结束】
21
【题目】已知定义在![]() 上的函数
上的函数![]() (
(![]() ),并且它在
),并且它在![]() 上的最大值为
上的最大值为![]()
(1)求![]() 的值;
的值;
(2)令![]() ,判断函数
,判断函数![]() 的奇偶性,并求函数
的奇偶性,并求函数![]() 的值域.
的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项均为正数的数列{an}的前n项和为Sn , 向量 ![]() =(Sn , an+1),
=(Sn , an+1), ![]() =(an+1,4)(n∈N*),且
=(an+1,4)(n∈N*),且 ![]() ∥
∥ ![]()
(1)求{an}的通项公式
(2)设f(n)=  bn=f(2n+4),求数列{bn}的前n项和Tn .
bn=f(2n+4),求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC 内部取n 个点, 将△ABC剖分为若干个小三角形(每两个小三角形或者有一个公共顶点,或者有一条公共边,或者完全没有公共点,如图所示).现将点A 染红色, 点B 染蓝色,点C 染黑色,其余n 个点的每个点也任意染上红、蓝、黑三色之一.我们称三个顶点的颜色恰为红、蓝、黑的小三角形为“特征三角形”.证明:至少有一个小三角形是特征三角形.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的一段图象如右图所示:
的一段图象如右图所示:

(1)求函数![]() 的解析式及其最小正周期;
的解析式及其最小正周期;
(2)求使函数取得最大值的自变量![]() 的集合及最大值;
的集合及最大值;
(3)求函数![]() 在
在![]() 的单调递增区间.
的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某企业生产的某种产品中抽取100件,测量这些产品的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间![]() ,
,![]() ,
,![]() 内的频率之比为
内的频率之比为![]() .
.

(Ⅰ)求这些产品质量指标值落在区间![]() 内的频率;
内的频率;
(Ⅱ)用分层抽样的方法在区间![]() 内抽取一个容量为6的样本,将该样本看成一个总体,从中任意
内抽取一个容量为6的样本,将该样本看成一个总体,从中任意
抽取2件产品,求这2件产品都在区间![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆x2+y2=8内有一点P(-1,2),AB为过点P且倾斜角为α的弦.

(1)当弦AB被点P平分时,求直线AB的方程;
(2)求过点P的弦的中点M的轨迹方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com