
【题目】图1是矩形![]() ,
,![]() ,
,![]() ,M为
,M为![]() 的中点,将
的中点,将![]() 沿
沿![]() 翻折,得到四棱锥
翻折,得到四棱锥![]() ,如图2.
,如图2.
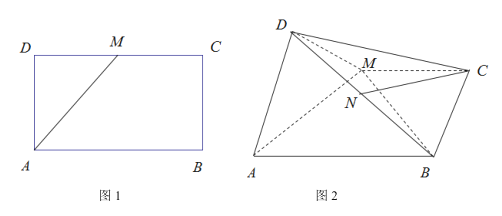
(Ⅰ)若点N为![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(Ⅱ)若![]() .求点A到平面
.求点A到平面![]() 的距离.
的距离.
科目:高中数学 来源: 题型:
【题目】某校拟从甲、乙两名同学中选一人参加疫情知识问答竞赛,于是抽取了甲、乙两人最近同时参加校内竞赛的十次成绩,将统计情况绘制成如图所示的折线图.根据该折线图,下面结论正确的是( )
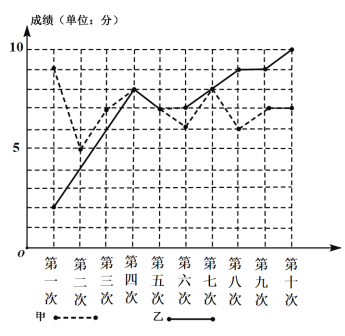
A.甲、乙成绩的中位数均为7
B.乙的成绩的平均分为6.8
C.甲从第四次到第六次成绩的下降速率要大于乙从第四次到第五次的下降速率
D.甲的成绩的方差小于乙的成绩的方差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为椭圆
为椭圆![]() 上的一点,F为椭圆的右焦点,且
上的一点,F为椭圆的右焦点,且![]() 垂直于x轴,不过原点O的直线
垂直于x轴,不过原点O的直线![]() 交椭圆于A,B两点,线段
交椭圆于A,B两点,线段![]() 的中点M在直线
的中点M在直线![]() 上.
上.
(1)求椭圆C的标准方程;
(2)当![]() 的面积最大时,求直线
的面积最大时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 的底面是等边三角形,
的底面是等边三角形,![]() 在底面ABC上的射影为
在底面ABC上的射影为![]() 的重心G.
的重心G.
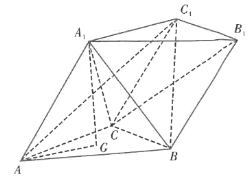
(1)已知![]() ,证明:平面
,证明:平面![]() 平面
平面![]() ;
;
(2)若三棱柱![]() 的侧棱与底面所成角的正切值为
的侧棱与底面所成角的正切值为![]() ,
,![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]() 、
、![]() .
.
(1)若![]() ,且函数
,且函数![]() 的图象是函数
的图象是函数![]() 图象的一条切线,求实数
图象的一条切线,求实数![]() 的值;
的值;
(2)若不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若对任意实数![]() ,函数
,函数![]() 在
在![]() 上总有零点,求实数
上总有零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足:a1=0,![]() (n∈N*),前n项和为Sn (参考数据: ln2≈0.693,ln3≈1.099),则下列选项中错误的是( )
(n∈N*),前n项和为Sn (参考数据: ln2≈0.693,ln3≈1.099),则下列选项中错误的是( )
A.![]() 是单调递增数列,
是单调递增数列,![]() 是单调递减数列B.
是单调递减数列B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com