
【题目】执行如图的程序框图,则输出S的值为( ) 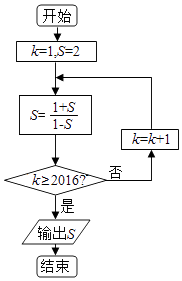
A.2
B.﹣3
C.﹣ ![]()
D.![]()
【答案】A
【解析】解:模拟执行程序,可得 S=2,k=1,S=﹣3,
不满足条件k≥2016,k=2,S=﹣ ![]() ,
,
不满足条件k≥2016,k=3,S= ![]() ,
,
不满足条件k≥2016,k=4,S=2,
不满足条件k≥2016,k=5,S=﹣3,
…
观察规律可知,S的取值周期为4,由于2016=504×4,可得
不满足条件k≥2016,k=2016,S=2,
满足条件k≥2016,满足退出循环的条件,
故输出的S值为2.
故选:A.
【考点精析】关于本题考查的程序框图,需要了解程序框图又称流程图,是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形;一个程序框图包括以下几部分:表示相应操作的程序框;带箭头的流程线;程序框外必要文字说明才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】已知f(x)为定义在[﹣1,1]上的奇函数,当x∈[﹣1,0]时,函数解析式为 ![]() . (Ⅰ)求f(x)在[0,1]上的解析式;
. (Ⅰ)求f(x)在[0,1]上的解析式;
(Ⅱ)求f(x)在[0,1]上的最值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知倾斜角60°为的直线l平分圆:x2+y2+2x+4y﹣4=0,则直线l的方程为( )
A.![]() x﹣y+
x﹣y+ ![]() +2=0
+2=0
B.![]() x+y+
x+y+ ![]() +2=0
+2=0
C.![]() x﹣y+
x﹣y+ ![]() ﹣2=0
﹣2=0
D.![]() x﹣y﹣
x﹣y﹣ ![]() +2=0
+2=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆心在直线x+y﹣1=0上且过点A(2,2)的圆C1与直线3x﹣4y+5=0相切,其半径小于5.
(1)若C2圆与圆C1关于直线x﹣y=0对称,求圆C2的方程;
(2)过直线y=2x﹣6上一点P作圆C2的切线PC,PD,切点为C,D,当四边形PCC2D面积最小时,求直线CD的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(0,﹣2),椭圆E: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,F是椭圆E的右焦点,直线AF的斜率为
,F是椭圆E的右焦点,直线AF的斜率为 ![]() ,O为坐标原点
,O为坐标原点
(1)求E的方程
(2)设过点A的动直线l与E相交于P,Q两点,问:是否存在直线l,使以PQ为直径的圆经过点原点O,若存在,求出对应直线l的方程,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中正确的是( )
A.奇函数f(x)的图象经过(0,0)点
B.y=|x+1|+|x﹣1|(x∈(﹣4,4])是偶函数
C.幂函数y=x ![]() 过(1,1)点
过(1,1)点
D.y=sin2x(x∈[0,5π])是以π为周期的函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的程序框图所表示的算法功能是输出( ) 
A.使1×2×4×6××n≥2017成立的最小整数n
B.使1×2×4×6××n≥2017成立的最大整数n
C.使1×2×4×6××n≥2017成立的最小整数n+2
D.使1×2×4×6××n≥2017成立的最大整数n+2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M的圆心在直线x﹣2y+4=0上,且与x轴交于两点A(﹣5,0),B(1,0). (Ⅰ)求圆M的方程;
(Ⅱ)求过点C(1,2)的圆M的切线方程;
(Ⅲ)已知D(﹣3,4),点P在圆M上运动,求以AD,AP为一组邻边的平行四边形的另一个顶点Q轨迹方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com