
【题目】已知椭圆E的中心在原点,焦点在x轴上,椭圆的左顶点坐标为![]() ,离心率为
,离心率为![]() .
.
![]() 求椭圆E的方程;
求椭圆E的方程;
![]() 过点
过点![]() 作直线l交E于P、Q两点,试问:在x轴上是否存在一个定点M,使
作直线l交E于P、Q两点,试问:在x轴上是否存在一个定点M,使![]() 为定值?若存在,求出这个定点M的坐标;若不存在,请说明理由.
为定值?若存在,求出这个定点M的坐标;若不存在,请说明理由.
科目:高中数学 来源: 题型:
【题目】某百货商场举行年终庆典,推出以下两种优惠方案:
方案一:单笔消费每满200元立减50元,可累计;
方案二:单笔消费满200元可参与一次抽奖活动,抽奖规则如下:从装有6个小球(其中3个红球3个白球,它们除颜色外完全相同)的盒子中随机摸出3个小球,若摸到3个红球则按原价的5折付款,若摸到2个红球则按原价的7折付款,若摸到1个红球则按原价的8折付款,若未摸到红球按原价的9折付款。
单笔消费不低于200元的顾客可从中任选一种优惠方案。
(I)某顾客购买一件300元的商品,若他选择优惠方案二,求该顾客最好终支付金额不超过250元的概率。
(II)若某顾客的购物金额为210元,请用所学概率知识分析他选择哪一种优惠方案更划算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】4男3女站成一排,求满足下列条件的排法共有多少种?
![]() 任何两名女生都不相邻,有多少种排法?
任何两名女生都不相邻,有多少种排法?
![]() 男甲不在首位,男乙不在末位,有多少种排法?
男甲不在首位,男乙不在末位,有多少种排法?
![]() 男生甲、乙、丙顺序一定,有多少种排法?
男生甲、乙、丙顺序一定,有多少种排法?
![]() 男甲在男乙的左边
男甲在男乙的左边![]() 不一定相邻
不一定相邻![]() 有多少种不同的排法?
有多少种不同的排法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的中心在原点,一个长轴端点为![]() ,离心率
,离心率![]() ,过P分别作斜率为
,过P分别作斜率为![]() 的直线PA,PB,交椭圆于点A,B。
的直线PA,PB,交椭圆于点A,B。
(1)求椭圆的方程;
(2)若![]() ,则直线AB是否经过某一定点?
,则直线AB是否经过某一定点?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,其图象在点
,其图象在点![]() 处切线的斜率为-3.
处切线的斜率为-3.
(1)求![]() 与
与![]() 关系式;
关系式;
(2)求函数![]() 的单调区间(用只含有
的单调区间(用只含有![]() 的式子表示);
的式子表示);
(3)当![]() 时,令
时,令![]() ,设
,设![]() 是函数
是函数![]() 的两个零点,
的两个零点, ![]() 是
是![]() 与
与![]() 的等差中项,求证:
的等差中项,求证: ![]() (
(![]() 为函数
为函数![]() 的导函数).
的导函数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[2019·吉林期末]一个袋中装有6个大小形状完全相同的球,球的编号分别为1,2,3,4,5,6.
(1)从袋中随机抽取两个球,求取出的球的编号之和为6的概率;
(2)先后有放回地随机抽取两个球,两次取的球的编号分别记为![]() 和
和![]() ,求
,求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是![]() 中点(如图1).将
中点(如图1).将![]() 沿
沿![]() 折起到图2中
折起到图2中![]() 的位置,得到四棱锥
的位置,得到四棱锥![]() .
.
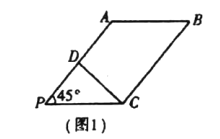
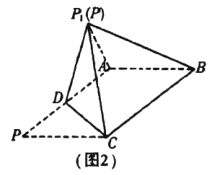
(1)将![]() 沿
沿![]() 折起的过程中,
折起的过程中, ![]() 平面
平面![]() 是否成立?并证明你的结论;
是否成立?并证明你的结论;
(2)若![]() 与平面
与平面![]() 所成的角为60°,且
所成的角为60°,且![]() 为锐角三角形,求平面
为锐角三角形,求平面![]() 和平面
和平面![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年“双节”期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速![]() 分成六段:
分成六段: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 后得到如图的频率分布直方图.
后得到如图的频率分布直方图.
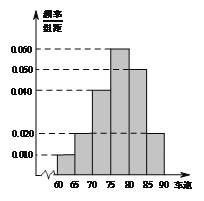
(I)某调查公司在采样中,用到的是什么抽样方法?
(II)求这40辆小型车辆车速的众数、中位数及平均数的估计值;
(III)若从车速在![]() 的车辆中任抽取2辆,求车速在
的车辆中任抽取2辆,求车速在![]() 的车辆至少有一辆的概率.
的车辆至少有一辆的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com